18. Sparse Signal Models

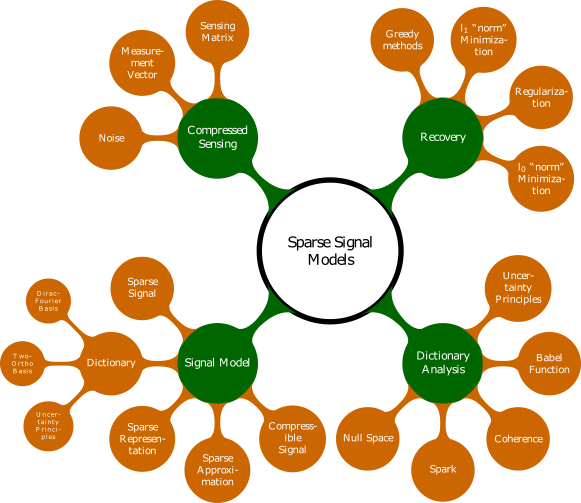
18.1. Outline

In this chapter we develop initial concepts of sparse signal models.

We begin our study with a review of solutions of under-determined systems. We build a case for solutions which promote sparsity.

We show that although the real life signals may not be sparse yet they are compressible and can be approximated with sparse signals.

We then review orthonormal bases and explain the inadequacy of those bases in exploiting the sparsity in many signals of interest. We develop an example of Dirac Fourier basis as a two ortho basis and demonstrate how it can better exploit signal sparsity compared to Dirac basis and Fourier basis individually.

We follow this with a general discussion of redundant signal dictionaries. We show how they can be used to create sparse and redundant signal representations.

We study various properties of signal dictionaries which are useful in characterizing the capabilities of a signal dictionary in exploiting signal sparsity.

In this chapter, our signals of interest will typically lie in the finite $N$-dimensional real or complex vector space ${\mathbb{R}}^N$ or ${\mathbb{C}}^N$. Sometimes we will restrict our attention to the $N$ dimensional Euclidean space to simplify discussion.

We will be concerned with different representations of our signals of interest in ${\mathbb{C}}^D$ where $D\ge N$. This aspect will become clearer as we go along in this chapter.

18.2. Sparsity

We quickly define the notion of sparsity in a signal.

We recall the definition of $l_0$-“norm” (don’t forget the quotes) of $\mathbf{x}\in {\mathbb{C}}^N$ given by

$$\Vert \mathbf{x}{\Vert }_0=\mathrm{card}(\mathrm{supp}(\mathbf{x}))$$

where $\mathrm{supp}(x)=\{i:x_i\ne 0\}$ denotes the support of $\mathbf{x}$ and $\mathrm{card}$ denotes the cardinality of a set. Informally we say that a signal $\mathbf{x}\in {\mathbb{C}}^N$ is sparse if $\Vert \mathbf{x}{\Vert }_0\ll N$.

More generally if

$$\mathbf{x}=\mathcal{D}\alpha$$

where $\mathcal{D}\in {\mathbb{C}}^{N\times D}$ with $D>N$ is some signal dictionary (to be formally defined later), then $\mathbf{x}$ is sparse in dictionary $\mathcal{D}$ if $\Vert \alpha {\Vert }_0\ll D$.

Sometimes we simply say that $\mathbf{x}$ is $K$-sparse if $\Vert \mathbf{x}{\Vert }_0\le K$ where $K<N$. We do not specifically require that $K\ll N$.

An even more general definition of sparsity is the degrees of freedom a signal may have.

Example 18.1 (Degrees of freedom on the surface of a sphere)

1. Consider all points on the surface of a unit sphere in ${\mathbb{R}}^N$.

2. For every point $\mathbf{x}$ belonging to the surface, we have $\Vert \mathbf{x}{\Vert }_2=1$.

3. Thus if we choose the values of $N-1$ components of $\mathbf{x}$ then the value of the remaining component is automatically fixed.

4. Thus the number of degrees of freedom $\mathbf{x}$ has on the surface of the unit sphere in ${\mathbb{R}}^N$ is $N-1$.

5. Such a surface represents a manifold in the ambient Euclidean space.

6. Of special interest are low dimensional manifolds where the number of degrees of freedom $K\ll N$.