Sensing Matrices
Contents
19.1. Sensing Matrices#
19.1.1. Matrices Satisfying RIP#
This section provides basic results about construction of matrices which can satisfy restricted isometry property.
The goal of designing an
Stable embedding for signals with has high sparsity as possible (high
As few measurements as possible (low
There are two different approaches
Deterministic approach
Randomized approach
Known deterministic approaches so far tend to require
Construction process:
Input
Generate
Suppose that
It can be shown that the rank of
Example 19.1 (Random matrices are full rank.)
We can verify this fact by doing a small computer simulation.
M = 6;
N = 20;
trials = 10000;
numFullRankMatrices = 0;
for i=1:trials
% Create a random matrix of size M x N
A = rand(M,N);
% Obtain its rank
R = rank(A);
% Check whether the rank equals M or not
if R == M
numFullRankMatrices = numFullRankMatrices + 1;
end
end
fprintf('Number of trials: %d\n',trials);
fprintf('Number of full rank matrices: %d\n',numFullRankMatrices);
percentage = numFullRankMatrices*100/trials;
fprintf('Percentage of full rank matrices: %.2f %%\n', percentage);
This program generates a number of random matrices and measures their ranks. It verifies whether they are full rank or not.
Here is a sample output:
>> demoRandomMatrixRank
Number of trials: 10000
Number of full rank matrices: 10000
Percentage of full rank matrices: 100.00
Thus if we choose
We can start with a chosen value of
Before we proceed further, we should take a detour and review sub-Gaussian distributions in Subgaussian Distributions.
We now state the main theorem of this section.
Theorem 19.1 (Norm bounds on subgaussian vectors)
Suppose that
Moreover, for any
and
19.1.1.1. Conditions on Random Distribution for RIP#
Let us get back to our business of constructing a matrix
We require that the distribution will yield a matrix that is norm-preserving. This requires that
(19.1)#Hence variance of distribution should be
We require that distribution is a sub-Gaussian distribution; i.e., there exists a constant
This says that the moment generating function of the distribution
is dominated by a Gaussian distribution.
In other words, tails of the distribution decay at least as fast as the tails of a Gaussian distribution.
We will further assume that entries of
Under these conditions we have the following result.
Corollary 19.1 (Norm bounds on subgaussian matrix vector product)
Suppose that
Let
and
where
This means that the norm of a sub-Gaussian random vector strongly concentrates about its mean.
19.1.1.2. Sub Gaussian Matrices satisfy the RIP#
Using this result we now state that sub-Gaussian matrices satisfy the RIP.
Theorem 19.2 (Lower bound on required number of measurements)
Fix
then
We note that this theorem achieves
This is much better than deterministic approaches.
19.1.1.3. Advantages of Random Construction#
There are a number of advantages of the random sensing matrix construction approach:
One can show that for random construction, the measurements are democratic. This means that all measurements are equal in importance and it is possible to recover the signal from any sufficiently large subset of the measurements.
Thus by using random
In general we are more interested in
Deterministic construction would explicitly require taking
But if
If
Thus if
Similar results hold for other sub-Gaussian distributions as well.
19.1.2. Rademacher Sensing Matrices#
In this subsection, we collect several results related to Rademacher sensing matrices.
Definition 19.1
A Rademacher sensing matrix
Thus
We can remove the scale factor
With that we can draw individual entries of
Thus entries in
This construction is useful since it allows us to implement the multiplication
with
We note that
Actually we have a better result with
We can write
where
In this case we also have
Thus the squared length of each of the columns in
Lemma 19.1
Let
Representative values of this bound are plotted below.
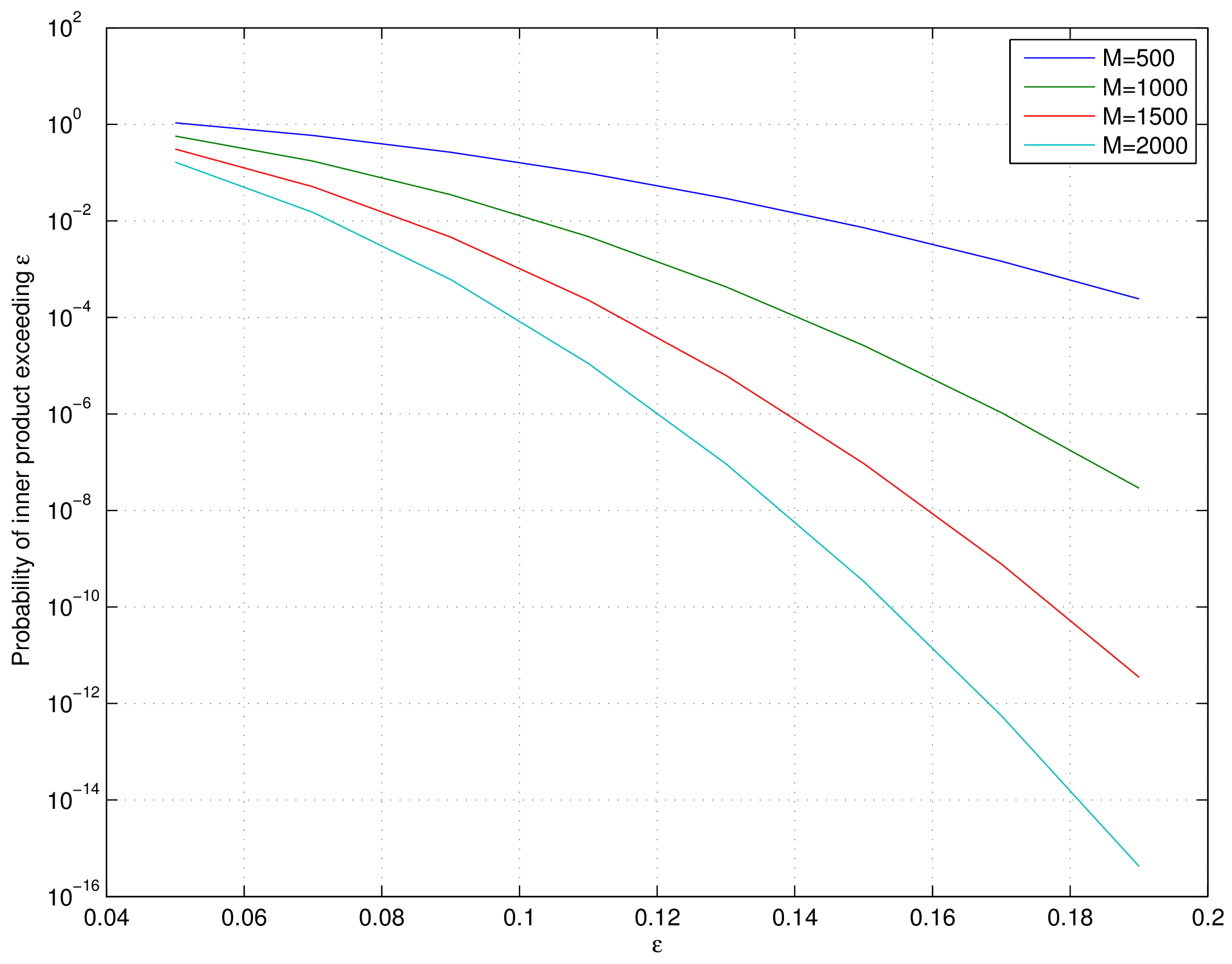
Fig. 19.1 Tail bound for the probability of inner product of a Rademacher random vector with a unit norm vector#
Proof. This can be proven using Hoeffding’s inequality. To be elaborated later.
A particular application of this lemma is when
The lemma establishes that the probability of inner product of two independent unit norm Rademacher random vectors being large is very very small. In other words, independently chosen unit norm Rademacher random vectors are incoherent with high probability. This is a very useful result as we will see later in measurement of coherence of Rademacher sensing matrices.
19.1.2.1. Joint Correlation#
Columns of
Lemma 19.2
Let
Proof. Let us call
We note that if for any
Thus if we prove the bound for vectors
Hence we will assume that
From Lemma 19.1 we have
Now the event
i.e. if any of the inner products (absolute value) is greater than
We recall Boole’s inequality which states that
Thus
This gives us
19.1.2.2. Coherence#
We show that coherence of Rademacher sensing matrix is fairly small with high probability (adapted from [80]).
Lemma 19.3
Fix
with probability exceeding
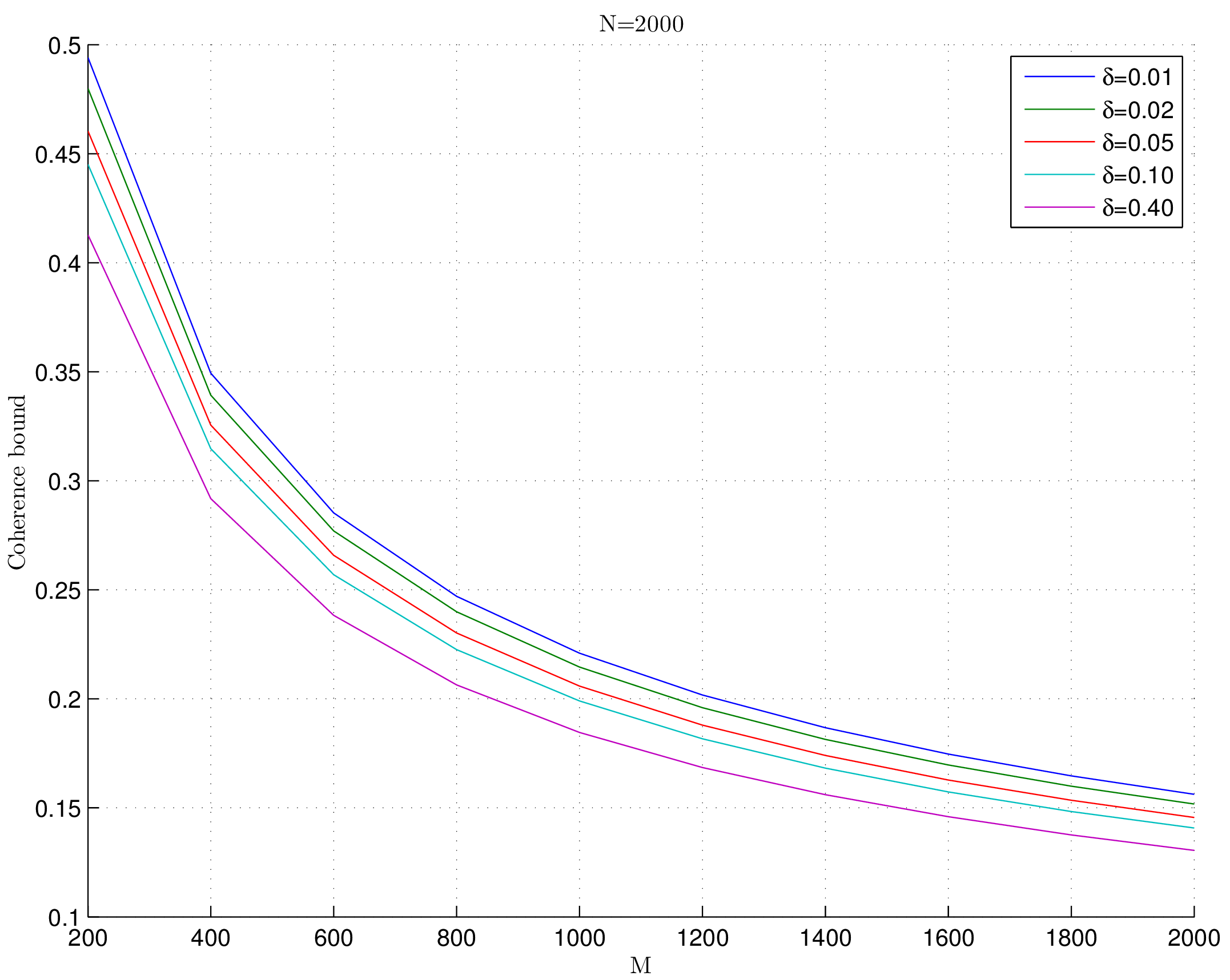
Fig. 19.2 Coherence bounds for Rademacher sensing matrices#
Proof. We recall the definition of coherence as
Since
Consider some
We note that they are independent of each other.
Thus from Lemma 19.1 we have
Now there are
Hence by applying Boole’s inequality
Thus we have
What we need to do now is to choose a suitable value of
We choose
This gives us
Putting back we get
This justifies why we need
Finally
and
which completes the proof.
19.1.3. Gaussian Sensing Matrices#
In this subsection we collect several results related to Gaussian sensing matrices.
Definition 19.2
A Gaussian sensing matrix
We note that
We can write
where
Thus the expected value of squared length of each of the columns in
19.1.3.1. Joint Correlation#
Columns of
Lemma 19.4
Let
Proof. Let us call
We note that if for any
Thus if we prove the bound for vectors
Hence we will assume that
Now consider
Since
Since
We recall a well known tail bound for Gaussian random variables which states that
Now the event
i.e. if any of the inner products (absolute value) is greater than
We recall Boole’s inequality which states that
Thus
This gives us