Convex Sets
Contents
9.2. Convex Sets#
Throughout this section, we assume that
9.2.1. Line Segments#
Definition 9.5 (Line segment)
Let
form a (closed) line-segment between
Similarly, we define an open line segment as:
The half-open segment
The half-open segment
9.2.2. Convex Sets#
Definition 9.6 (Convex set)
A set
The empty set is vacuously convex.
The entire vector space

Fig. 9.1 Examples of convex sets#
Observation 9.2
Since a convex set contains the line segment between any two points, any line segment is convex by definition.
Geometrically, a convex set has no holes, hollows, pits or dimples. A set is convex if from each point in the set, it is possible to see every other point without having the line of sight pass outside the set.
Example 9.1 (Real line)
On the real line
Theorem 9.7
Any linear subspace is convex.
Proof. Let
Thus,
Theorem 9.8
Any affine set is convex.
Proof. Let
Theorem 9.9
Any hyperplane is convex since it is affine.
Theorem 9.10
Half spaces are convex.
Proof. Consider
Let
For some
Thus,
Theorem 9.11 (Convex set as convex combination of itself)
Let
In particular, if
Proof. The statement
Let
Then there exist
Hence
Hence
We now show the converse.
Let
Then there exist
If
Now assume that
By the convexity of
Hence
Hence
Together, we have
Theorem 9.12 (Convex set as union of line segments)
Let
Proof. Let
If
So
We first show that
Let
Then
Hence
Hence
We now show the converse.
Let
Then there exists
Then by convexity of
Hence
Hence
Together,
9.2.3. Rays#
Definition 9.7 (Ray)
A ray
where
Theorem 9.13
A ray is convex.
Proof. Let a ray be given as:
Let
Now, for some
Since
9.2.4. Balls#
Proof. Recall that an open ball in a normed linear space is defined as:
Let
By triangle inequality:
Thus,
Theorem 9.15
A closed ball
Proof. Recall that a closed ball in a normed linear space is defined as:
Let
By triangle inequality:
Thus,
9.2.5. Convex Combinations#
Definition 9.8 (Convex combination)
We call a point of the form
It is like a weighted average of the points
Example 9.2 (Center of mass)
Consider a system of particles
Solving this equation gives us:
where
If we assign
which is a convex combination of the locations
Remark 9.2 (Convex combinations and unit simplex)
We recall that the unit simplex in
Thus, the coefficients for convex combinations of
Theorem 9.16 (Closure under convex combinations)
A set is convex if and only if it contains all convex combinations of its points.
Let
Proof. We know that a set
We first show that if
By definition
As induction hypothesis, assume that
Consider a convex combination of
where
Since
Without loss of generality, assume
Note that
Define
Note that
Thus,
By induction hypothesis,
Now,
Hence,
It is a 2 point convex combination of
Since both
Thus,
For the converse, note that if
Theorem 9.17
A convex combination of convex combinations is a convex combination.
Proof. Let
Consider
Let
Consider the convex combination
We need to show that
Towards this:
Consider the terms:
Since
Now, consider their sum:
Thus,
Hence,
is a convex combination of points of
9.2.6. Convex Hull#
Definition 9.9 (Convex hull)
The convex hull of an arbitrary set
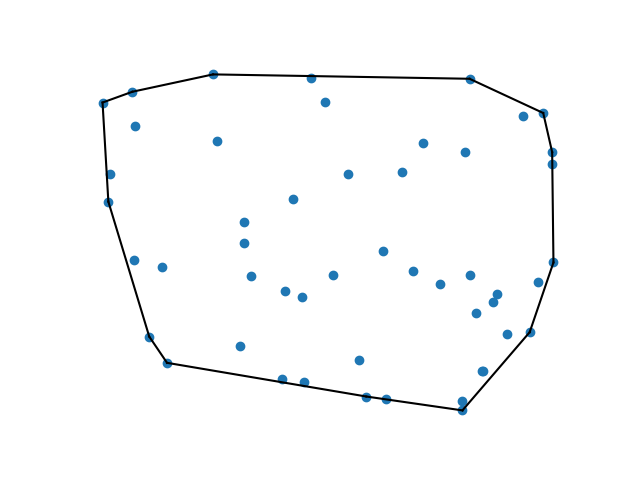
Fig. 9.2 The convex hull of a set of random points on the 2D plane#
Property 9.1 (Convexity of convex hull)
The convex hull
Proof. Let
Hence,
By Theorem 9.17, a convex combination of convex combinations is a convex combination.
Thus,
But
Hence,
Thus,
Property 9.2 (Affine hull of convex hull)
Let
In other words, the affine hull of a set and its convex hull are identical.
Proof. By using a translation argument if necessary,
without loss of generality, we assume that
Then both
Since
For the converse, assume that
Let
Then for every
By definition of convex hull, each
Hence every
Hence
Theorem 9.18
The convex hull of a set
Proof. Let
Let
Then,
Hence,
Thus, in particular
Since
We could have started as defining the convex hull of
9.2.6.1. Carathéodory Theorem#
Theorem 9.19 (Carathéodory theorem)
Let
Then, there exists a set of
i.e., there exists a
Proof. We note that
Thus, there exists a set of
We can assume
If
Hence, consider the case where
We now describe a process which can reduce the number of points in the convex combination by one.
The
Thus, there is a nontrivial linear combination of these vectors
Let
with
In particular, there exists at least one index
Let
Then,
with
Thus, it is a convex combination for
Let
Then,
Also, we can see that
Thus, we have found a convex combination for
Thus, we have obtained a convex combination for
Repeating this process up to
9.2.7. Dimension#
Definition 9.10 (Dimension of a convex set)
The dimension of a convex set is defined to be the dimension of its affine hull.
If
Recall that the dimension of an affine set is equal to the dimension of the linear subspace associated with it (Definition 4.163).
A circle will have a dimension of 2 even if it is in
A sphere will have a dimension of three.
9.2.8. Simplices#
Theorem 9.20 (Convex hull of a finite set of points)
Let
In
A Simplex is a convex hull of a finite set of affine independent points. The simplex provides a powerful coordinate system for the points within it in terms of barycentric coordinates.
Definition 9.11 (
Let
The simplex determined by them is given by
where
In other words,
A simplex is a convex set since it is a convex hull of its vertices.
Example 9.3 (Simplex examples)
In
A 0-simplex is a point.
A 1-simplex is a line segment (2 points).
A 2-simplex is a triangle (3 points).
A 3-simplex is a tetrahedron (4 points).
A 4-simplex is a 5-cell (5 points).
Theorem 9.21 (Barycentric coordinates)
Each point of a
Proof. Let
Let
Then,
For contradiction, assume there was another representation:
Then,
But
Hence,
Thus, the representation is unique.
Definition 9.12 (Simplex midpoint)
The point
Theorem 9.22
The dimension of a convex set
Proof. We need to show that there is a simplex
Let
Since
Thus,
Thus, if
Thus, if
Let
Then, there exist affine independent points
Let
Then,
If
That would lead to a set of
Hence,
Thus,
Since
Thus,
9.2.9. Symmetric Reflections#
The symmetric reflection of a convex set is convex since convexity is preserved under scalar multiplication. See Theorem 9.30 below.
If a symmetric convex set
contains a nonzero vector
9.2.10. Infinite Convex Combinations#
We can generalize convex combinations to include infinite sums.
Theorem 9.23
Let
and let
if the series converges.
We can generalize it further to density functions.
Theorem 9.24
Let
Then
provided the integral exists.
Note that
9.2.11. Convexity Preserving Operations#
In the following, we will discuss several operations which transform a convex set into another convex set, and thus preserve convexity.
Understanding these operations is useful for determining the convexity of a wide variety of sets.
Usually, it is easier to prove that a set is convex by showing that it is obtained by a convexity preserving operation from a convex set compared to directly verifying the convexity property i.e.
9.2.11.1. Intersection and Union#
Theorem 9.25 (Intersection of convex sets)
If
Proof. Let
Since
Similarly
Thus
which completes the proof.
We can generalize it further.
Theorem 9.26 (Intersection of arbitrary collection of convex sets)
Let
Proof. Let
Hence
Corollary 9.1 (Arbitrary intersection of closed half spaces)
Let
is convex.
Proof. Since each of the half spaces is convex, hence so is their intersection.
This result is applicable for open half spaces and hyperplanes too too. It also applies for a mixture of hyperplanes and half-spaces.
Corollary 9.2
The solution set of a system of linear equations and inequalities
in
Proof. We proceed as follows:
The solution set of each linear equation is a hyperplane.
The solution set of each linear inequality is a half-space (closed or open).
The solution set of a system of linear equations and inequalities is the intersection of these hyperplanes and half-spaces.
Each hyperplane and each half-space is convex.
Hence, their intersection is convex.
Theorem 9.27 (Intersection and union of two sets)
Let
Proof. Let
Let
Theorem 9.28 (Intersection and union of arbitrary sets)
Let
And, the smallest convex set containing every set of
Proof. Let
Let
9.2.11.2. Affine Functions#
Let us start with some simple results.
Theorem 9.29 (Convexity and translation)
Convexity is preserved under translation.
Proof. Let
Assume
Then, for every
Let
Let
Then,
Then,
But
Then,
Thus,
Thus,
We can follow the same argument in the opposite direction
to establish that
Theorem 9.30 (Convexity and scalar multiplication)
Convexity is preserved under scalar multiplication.
Proof. Let
Assume
Let
Let
Then,
Let
But
Hence,
Hence,
Thus,
Similar argument in opposite direction establishes
that
Recall that an
affine function
for every
Recall from Theorem 4.193 that an affine function can be written as a linear transformation followed by a translation:
where
Example 9.4
An affine function
where
Theorem 9.31 (Image under affine function)
Let
is a convex set.
Proof. We proceed as follows:
Let
Then,
Let
Then,
Since
Since
We have shown that for any
Thus,
It applies in the reverse direction also.
Theorem 9.32 (Inverse image under affine function)
Let
is convex.
Proof. Denote
We proceed as follows:
Let
Let
Let
Then,
Let
Since
Since
We have shown that for any
Thus,
Example 9.5 (Affine functions preserving convexity)
Let
For some
For some
Let
is convex. This is the projection operation. It projects vectors from
Example 9.6 (System of linear equations)
Consider the system of linear equations
If
The nonnegative orthant
Let
Then,
Thus, the solution set of a system of linear inequalities
of the form
Now, if
Theorem 9.33 (Orthogonal projection of convex set)
The orthogonal projection
of a convex set
Proof. We recall that orthogonal projection is a linear mapping and thus an affine function. By Theorem 9.31, image of a convex set under an affine function is convex. Hence proved.
9.2.11.3. Set Addition#
Theorem 9.34 (Convexity and set addition)
Let
Proof. We proceed as follows:
Let
Then,
Similarly,
Let
Then:
But,
Similarly,
Hence,
Thus,
One way to think geometrically about set addition is as the
union of all translates of
Theorem 9.35
A set
Proof. Assume
Thus,
For every
Thus,
Thus,
Combining, we get
Assume
Let
Then,
Hence,
Thus,
Theorem 9.36 (Convexity and linear combination)
Convexity is preserved under linear combinations.
Let
is convex.
Proof. Due to Theorem 9.30,
By (finite) repeated application of Theorem 9.34, their sum is also convex.
Theorem 9.37 (Nonnegative scalar multiplication distributive law)
Let
Proof. From Theorem 4.16, we know that:
We now show that
If both
If either of
Now, consider the case
Define
Then,
Then, since
Multiplying by
For the special case of
Some implications are
Theorem 9.38 (Convex combinations over arbitrary unions)
Let
i.e.,
where the union is taken over all finite convex combinations
(i.e. over all nonnegative choices of
Proof. We proceed as follows:
Let
Then,
Thus,
Drop all the terms from
If
Thus, terms from a single
Thus, we can simplify
such that each
Thus,
where
This is the same set as
Corollary 9.3 (Convex hull of union)
Let
Then,
9.2.11.4. Partial Addition#
Recall the notion of
direct sum
of two vector spaces
Theorem 9.39 (Partial addition on convex sets)
Let
Proof. Let
Let
Let
Let
Let
Since
Since
But then, we note that
Thus,
Thus,
We can write a version of the theorem above for
Corollary 9.4 (Partial addition on convex sets in Euclidean space)
Let
The relationship between
When
When
In between, we have a spectrum of results where for a vector in
In other words, if a vector space can be decomposed as a direct sum of two subspaces, then we have intersection or representation in one subspace while addition in the other.
This partial addition (binary) operation is commutative as well as associative.
Partial additions appear naturally
in convex cones in
9.2.11.5. Cartesian Product/Direct Sum#
Theorem 9.40 (Direct sum of convex sets)
Let
More generally, if
Proof. If either
Let
Then,
Since
Now,
Since
Thus,
Thus,
The generalization for multiple real vector spaces is easily verifiable through induction.
9.2.11.6. Projection#
Theorem 9.41 (Projection of a direct sum)
Let
More generally, if
Proof. Consider the case of two vector spaces
Let
Pick any
Then,
Since
Thus,
Thus,
Similarly
The argument can be extended by mathematical induction for multiple vector spaces.
Theorem 9.42 (Projection of a convex set)
Let
For every
Then
Similarly, if for every
then
Proof. If
Then for every
Let
Then
Since
i.e.,
This implies that
Hence
The argument for the convexity of
9.2.12. Extreme Points#
Definition 9.13 (Extreme points of convex sets)
Let
A point
In other words,
The set of extreme points of a set
Example 9.7 (Extreme points)
Let
Let
In a triangle, the three vertices are extreme points.
In a convex polytope, all the vertices are extreme points.
A more intricate example of the set
of extreme points for the set