Convex Functions
Contents
9.8. Convex Functions#
Throughout this section, we assume that
We suggest the readers to review the notions of graph, epigraph, sublevel sets of real valued functions in Real Valued Functions. Also pay attention to the notion of extended real valued functions, their effective domains, graphs and level sets.
9.8.1. Convexity of a Function#
Definition 9.43 (Convex function)
Let
An extended valued function
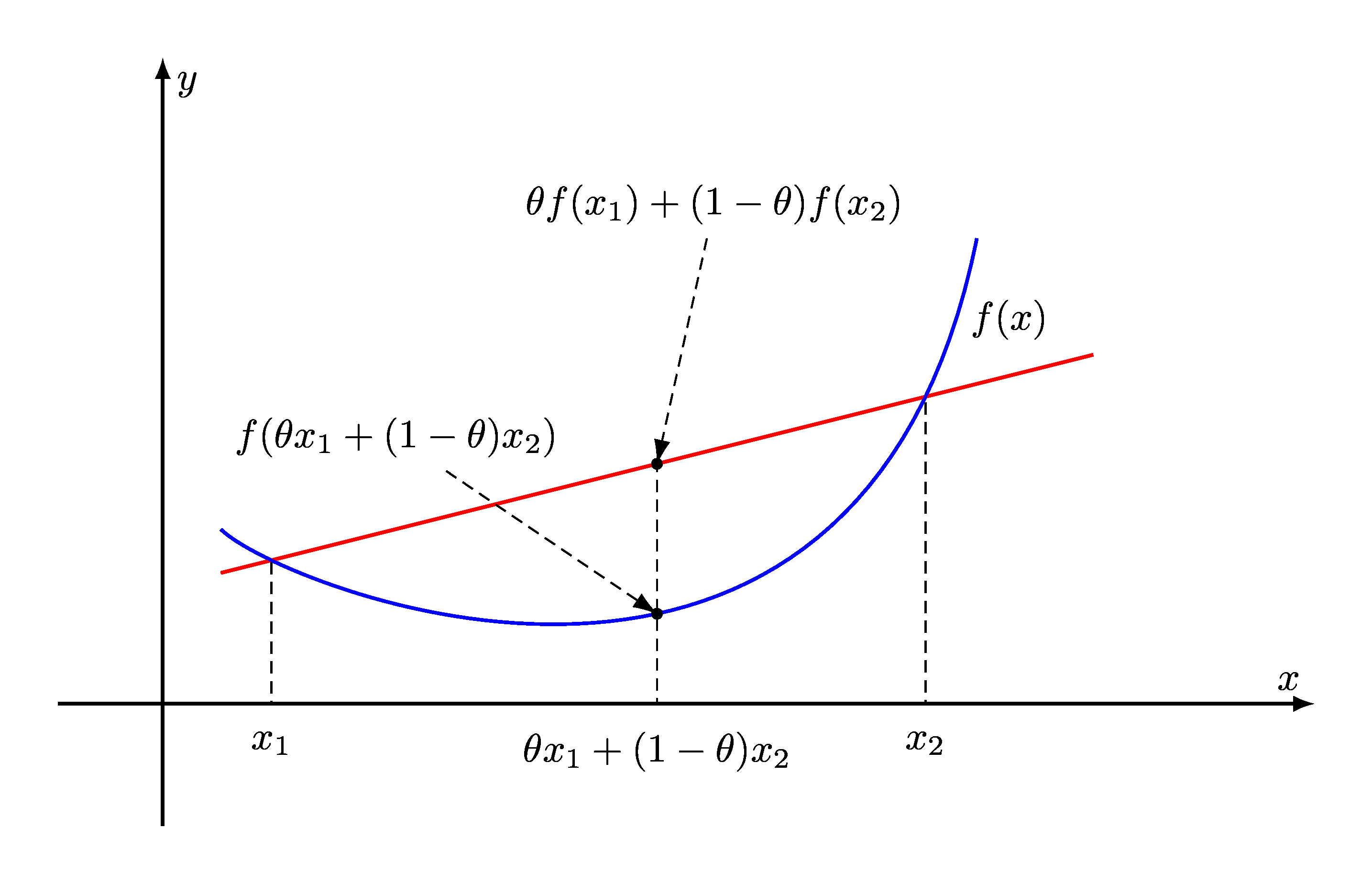
Fig. 9.3 Graph of a convex function. The line segment between any two points on the graph lies above the graph.#
For a convex function, every chord lies above the graph of the function.
9.8.1.1. Strictly Convex Functions#
Definition 9.44 (Strictly convex function)
Let
In other words, the inequality is a strict inequality
whenever the point
9.8.1.2. Concave Functions#
Definition 9.45 (Concave function)
We say that a function
Example 9.25 (Linear functional)
A linear functional on
i.e. the inner product of
Theorem 9.67
All linear functionals on a real vector space are convex as well as concave.
Proof. For any
Thus,
9.8.1.3. Arithmetic Mean#
Example 9.26 (Arithmetic mean is convex and concave)
Let
Arithmetic mean is a linear function. In fact
for all
Thus, for
Thus, arithmetic mean is both convex and concave.
9.8.1.4. Affine Function#
Example 9.27 (Affine functional)
An affine functional is a special type of
affine function
which maps a vector from
On real vector spaces, an affine functional on
i.e. the inner product of
Theorem 9.68
All affine functionals on a real vector space are convex as well as concave.
Proof. A simple way to show this is to recall that for any
affine function
holds true for any
In the particular case of real affine functionals,
for any
This establishes that
Another way to prove this is by following the definition
of
9.8.1.5. Absolute Value#
Example 9.28 (Absolute value is convex)
Let
with
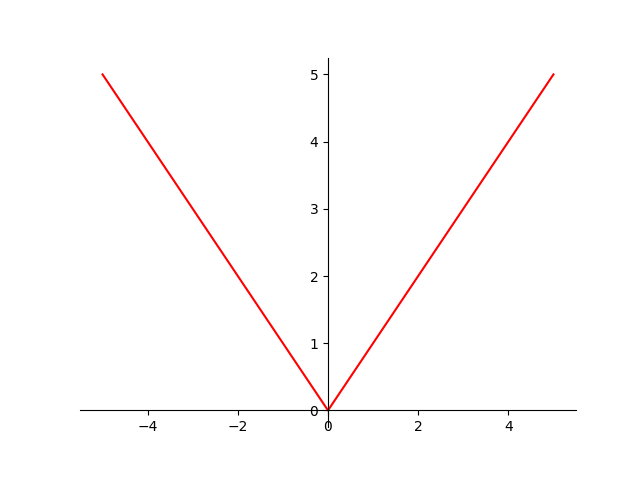
Recall that
In particular, for any
Thus
Hence,
9.8.1.6. Norms#
Theorem 9.69 (All norms are convex)
Let
In particular, for any
Thus
Fig. 9.4
Fig. 9.5
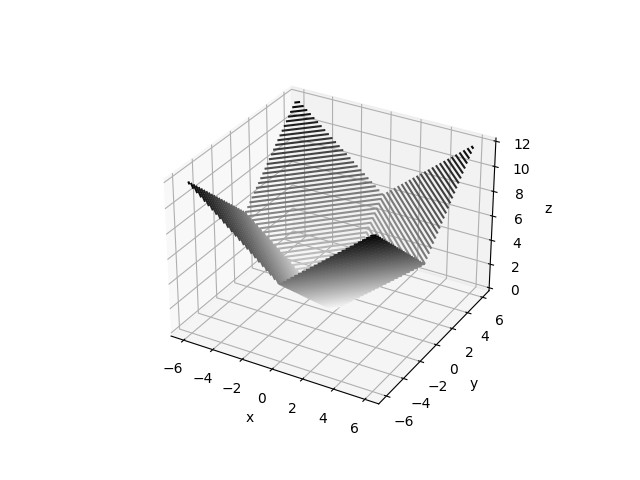
Fig. 9.6
Fig. 9.7
9.8.1.7. Max Function#
Example 9.29 (Max function is convex)
Let
with
Let
Let
Then, for every
Thus,
Taking maximum on the left hand side, we obtain:
But
Thus,
Thus,
9.8.1.8. Geometric Mean#
Example 9.30 (Geometric mean is concave)
Let
with
Recall from AM-GM inequality:
Let
Let
Note that
With
With
Multiplying the first inequality by
Recall that
Thus,
9.8.1.9. Powers#
Example 9.31 (Powers of absolute value)
Let
with
For
Consider the case where
Let
By triangle inequality:
We can write this as:
By Hölder's inequality, for some
Let
Applying Hölder’s inequality,
Taking power of
Which is the same as
Thus,
9.8.1.10. Empty Function#
Observation 9.4 (Empty function is convex)
Let
Proof. The empty set
This observation may sound uninteresting however
it is important in the algebra of convex functions.
Definition 2.48 provides
definitions for sum of two partial functions
and scalar multiplication with a partial
function. If two convex functions
Jensen's inequality, discussed later in the section, generalizes the notion of convexity of a function to arbitrary convex combinations of points in its domain.
9.8.2. Convexity on Lines in Domain#
Theorem 9.70 (
Let
In other words,
Proof. For any arbitrary
we have defined
with the domain:
Assume
Let
It means that there are
and
Let
Note that:
Since
Thus,
We have shown that if
Thus,
Now,
We showed that for any
Thus,
For the converse, we need to show that
if for any
Assume for contradiction that
We show that both of these conditions lead to contradictions.
Assume
Then, there exists
Let
Note that
Picking
Since
This contradicts the fact that
Thus,
We now accept that
Again, let
Pick
We have
In particular,
Since
We have a contradiction.
Thus,
A good application of this result is in showing the concavity of the log determinant function in Example 9.49 below.
9.8.3. Epigraph#
The epigraph
of a function
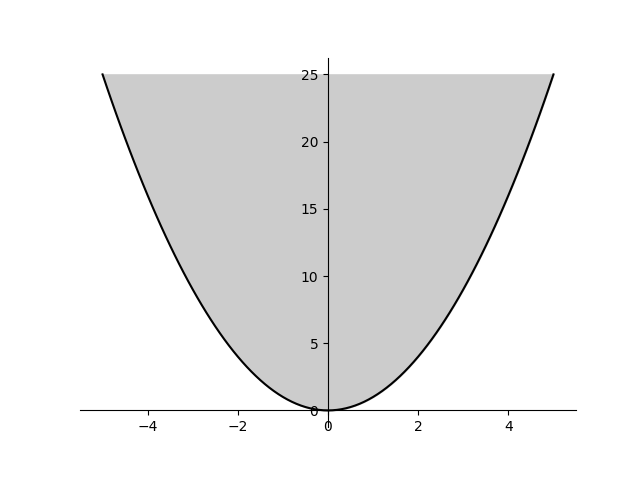
Fig. 9.8 Epigraph of the function
The definition of epigraph also applies for extended
real valued functions
9.8.3.1. Convex Functions#
Theorem 9.71 (Function convexity = Epigraph convexity)
Let
This statement is also valid for extended real valued functions.
Proof. Let
Assume
Let
Then,
Let
Consider the point
We have
And
Then,
Since
But then,
Thus,
Thus,
Thus,
Assume
Let
Let
Then,
Let
Let
Since
i.e.,
Thus,
Thus,
And,
But
Thus,
Thus,
Note that
Theorem 9.72 (Convex function from convex set by minimization)
Let
Then
Proof. We show the convexity of
Let
Then
By the definition of
Similarly, for every
Consider the sequences
By the convexity of
Hence for every
Taking the limit
Hence
Hence
Hence
9.8.3.2. Nonnegative Homogeneous Functions#
Recall that a real valued function
Theorem 9.73 (Nonnegative homogeneity = Epigraph is cone)
A function
Proof. Let
Let
Let
Then,
But
Thus,
Thus,
Assume
Let
Then,
Since
Now, let
Since
Then,
By definition of epigraph,
We claim that
Assume for contradiction that
Then,
Since
But then,
Hence,
9.8.3.3. Nonnegative Homogeneous Convex Functions#
Theorem 9.74 (Nonnegative homogeneous convex function epigraph characterization)
Let
Proof. By Theorem 9.73,
By Theorem 9.71,
Thus,
Theorem 9.75 (Nonnegative homogeneous convex function is subadditive)
Let
Proof. Assume that
By Theorem 9.74,
Then, by Theorem 9.47
Pick any
Then
Then, their sum
This means that
Now for the converse, assume that
By Theorem 9.73,
Consequently, it is closed under nonnegative scalar multiplication.
Pick any
Let
Then,
Now,
Since
Thus,
We have shown that for any
Thus,
Since
But then, by Theorem 9.74,
Corollary 9.5
Let
Proof. Since
Thus,
But,
Thus,
Thus,
Theorem 9.76 (Linearity of nonnegative homogeneous functions)
Let
If
Proof. We are given that
Assume that
Now, for the converse, assume that
Let
Then,
Also,
But
Thus,
Combining, we get
For any
Thus, for any
Thus,
Since
Finally, assume that
By previous argument
Let
Then,
Since
This can hold only if all the inequalities are equalities in the previous derivation.
Thus,
Then, following the previous argument,
9.8.4. Extended Value Extensions#
Tracking domains of convex functions is difficult.
It is often convenient to extend a convex function
Definition 9.46 (Extended value extension)
The extended value extension
of a convex function
We mention that the defining inequality (9.1)
for a convex function
At
Since
The inequality then reduces to (9.1).
If either
Definition 9.47 (Effective domain)
The effective domain
of an extended valued function
An equivalent way to define the effective domain is:
Theorem 9.77 (Effective domain and sum of functions)
If
Proof. We proceed as follows:
At any
Thus,
Hence,
At any
Thus,
Thus,
Several commonly used convex functions have vastly different domains. If we work with these functions directly, then we have to constantly worry about identifying the domain and manipulating the domain as per the requirements of the operations we are considering. This quickly becomes tedious.
An alternative approach is to work with the
extended value extensions of all functions.
We don’t have to worry about tracking the function
domain. The domain can be identified whenever needed
by removing the parts from
In this book, unless otherwise specified, we shall assume that the functions are being treated as their extended value extensions.
9.8.5. Proper Functions#
Definition 9.48 (Proper function)
An extended real-valued function
In other words,
Putting another way, a proper function
is obtained by taking a real valued function
It is easy to see that the codomain for a proper
function can be changed from
Definition 9.49 (Improper function)
An extended real-valued function
For an improper function
Most of our study is focused on proper functions. However, improper functions sometimes do arise naturally in convex analysis.
Example 9.32 (An improper function)
Consider a function
Then,
9.8.6. Indicator Functions#
Definition 9.50 (Indicator function)
Let
The extended value extension of an indicator function is given by:
Theorem 9.78 (Indicator functions and convexity)
An indicator function is convex if and only if its domain is a convex set.
Proof. Let
since
Thus,
If
Theorem 9.79 (Restricting the domain of a function)
Let
Also,
The statement is obvious. And quite powerful.
The problem of minimizing a function
9.8.7. Sublevel Sets#
Recall from Definition 2.53
that the
The strict sublevel sets for a real valued function
The sublevel sets can be shown to be intersection of a set of strict sublevel sets.
Theorem 9.80 (Sublevel set as intersection)
Let
denote the strict sublevel set of
denote the sublevel set of
Proof. We show that
Let
Then,
Thus,
Thus,
Thus,
We now show that
Let
Then,
Taking the infimum on the R.H.S. over the set
Thus,
Thus,
Theorem 9.81 (Convexity of sublevel sets)
If
are convex.
Proof. Assume
Let
Then,
Let
Let
Since
Thus,
Thus,
Thus,
The converse is not true. A function need not be convex even if all its sublevel sets are convex.
Example 9.33
Consider the function
Its sublevel sets are convex as they are intervals.
Theorem 9.82 (Convexity of strict sublevel sets)
If
are convex.
Proof. Assume
Let
Then,
Let
Let
Since
Thus,
Thus,
Thus,
An alternate proof for showing the convexity of the sublevel sets is to show it as an intersection of strict sublevel sets.
Theorem 9.83 (Intersection of sublevel sets of convex functions)
Let
is a convex set.
Proof. For each
Then,
Thus,
Example 9.34 (Convexity of sublevel sets of the quadratic)
Let
Consider the sets of the form
This is a sublevel set of the quadratic function
Since
Sets of this form include the solid ellipsoids, paraboloids as well as spherical balls. Here is an example of the spherical ball of the norm induced by the inner product.
9.8.8. Hypograph#
The hypograph
of a function
Just like function convexity is connected to epigraph convexity, similarly function concavity is connected to hypograph convexity.
Theorem 9.84 (Function concavity = Hypograph convexity)
A function
Proof.
9.8.9. Super-level Sets#
Recall from Definition 2.56
that the
Theorem 9.85
If
Proof. Assume
Let
Then,
Let
Let
Since
Thus,
Thus,
Thus,
The converse is not true. A function need not be concave even if all its super-level sets are convex.
Example 9.35
Let geometric mean be given by:
with
Let arithmetic mean be given by:
Consider the set:
In Example 9.30 we establish that
In Example 9.26 we established that
Thus,
Thus,
Note that
Thus,
Since
9.8.10. Closed Convex Functions#
Recall from Real Valued Functions that a function is closed if all its sublevel sets are closed. A function is closed if and only if its epigraph is closed. A function is closed if and only if it is lower semicontinuous.
In general, if a function is continuous, then it is lower semicontinuous and hence it is closed.
In this subsection, we provide examples of convex functions which are closed.
9.8.10.1. Affine Functions#
Theorem 9.86 (Affine functions are closed)
Let
where
Proof. We prove closedness by showing that the epigraph of
Let
Let
We have
In other words
Taking the limit on both sides, we get
Hence
Hence
Hence
9.8.10.2. Norms#
Theorem 9.87 (All Norms are closed)
Let
Proof. The sublevel sets are given by
9.8.11. Support Functions#
Definition 9.51 (Support function for a set)
Let
Since
Example 9.36 (Finite sets)
Let
This follows directly from the definition.
9.8.11.1. Convexity#
Theorem 9.88 (Convexity of support function)
Let
Proof. Fix a
is a pointwise supremum of convex functions.
By Theorem 9.114,
We note that the convexity of the support function
9.8.11.2. Closedness#
Theorem 9.89 (Closedness of support function)
Let
Proof. Recall that a function is closed if all its sublevel sets are closed.
Let
Consider the sublevel set
Then,
Thus,
Define
Then,
Now,
Thus,
Thus,
Thus, all sublevel sets of
Thus,
9.8.11.3. Equality of Underlying Sets#
Theorem 9.90 (Equality of underlying sets for support functions)
Let
Proof. If
For contradiction, assume that
Without loss of generality, assume that there exists
Since
Thus, there exists
Taking supremum over
Thus, there exists
This contradicts our hypothesis that
Thus,
9.8.11.4. Closure and Convex Hull#
The next result shows that support function
for a set and its closure or its convex hull
are identical. This is why, we required
Theorem 9.91 (Support functions and closure or convex hull of underlying set)
Let
Proof. We first consider the case of closure.
Thus,
Let us now show the reverse inequality.
Let
Then, there exists a sequence
Now for every
Thus,
Since
Taking the limit
Thus,
Since this is true for every
Now, consider the case of convex hull.
By definition,
Thus,
Let
Then, there exists a sequence
Since
By linearity of the inner product
Taking the limit
Thus,
Since this is true for every
9.8.11.5. Arithmetic Properties#
Following properties of support functions are useful in several applications.
Theorem 9.92 (Arithmetic properties of support functions)
(Nonnegative homogeneity) For any nonempty set
(Subadditivity) For any nonempty set
(Nonnegative scaling of the underlying set) For any nonempty set
(Additivity over Minkowski sum of sets) For any two nonempty subsets
Proof. (1) Nonnegative homogeneity
Here, we used the fact that
(2) Subadditivity
(3) Nonnegative scaling of the underlying set
(4) Minkowski sum
9.8.11.6. Cones#
Recall from Definition 9.22 that a set
Theorem 9.93 (Support function of a cone)
Let
In words, the support function of a cone
Proof. We proceed as follows
Assume that
Then,
In particular,
Accordingly,
Thus,
Now consider
Then, there exists
Since
Accordingly,
Taking the limit
Thus,
Thus,
Example 9.37 (Support function of nonnegative orthant)
Let
which is the nonpositive orthant
9.8.11.7. Affine Sets#
Theorem 9.94 (Support function for an affine set)
Let
Assume that
Proof. We proceed as follows.
By definition of support function
Introduce a variable
Then
Accordingly
where
We note that the statement
In other words,
The set
By Theorem 9.93, the support function of a cone is the indicator function of its polar cone.
By Theorem 9.66, the polar cone is given by
It is easy to see that
Every vector
Accordingly
This gives us
9.8.11.8. Norm Balls#
Theorem 9.95 (Support functions for unit balls)
Let
Then, the support function is given by
where
Proof. This flows directly from the definitions of support function and dual norm.
9.8.12. Gauge Functions#
Definition 9.52 (Gauge function for a set)
Let
If
The gauge function is also known as Minkowski functional.
Property 9.33 (Nonnegativity)
The Gauge function is always nonnegative.
Property 9.34 (Value at origin)
Property 9.35 (Subadditive)
If
Proof. We proceed as follows.
If
Then, the sets
Thus, we can choose some
If
and the inequality is satisfied.
Now, consider the case where
Then,
Now,
Thus,
Since
Thus,
Thus,
Thus, for every
Taking infimum on the R.H.S. over
Property 9.36 (Homogeneous)
The Gauge function is homogeneous.
Property 9.37 (Seminorm)
The Gauge function is a seminorm.
Example 9.38 (Norm as a gauge function)
Let
Let
Then,
The gauge function for the closed unit ball is simply the norm itself.
9.8.13. Jensen’s Inequality#
Jensen’s inequality stated below is another formulation for convex functions.
Theorem 9.96 (Jensen’s inequality)
A proper function
holds true for every
Proof. The Jensen’s inequality reduces to (9.1)
for
Assume
Let
If any of
Thus, we shall assume that
Since
Inductively, assume that the Jensen’s inequality holds for
holds true whenever
WLOG, assume that
Define
Note that
We can now write:
Thus,
For the converse, assume that
Thus,
Jensen’s inequality is essential in proving a number of famous inequalities.
Example 9.39 (Logarithm and Jensen’s inequality)
In Example 9.45, we show that
Now, let
Multiplying by
For a particular choice of
which is the AM-GM inequality suggesting that arithmetic mean is greater than or equal to the geometric mean for a group of positive real numbers.
Theorem 9.97 (Jensen’s inequality for nonnegative homogeneous convex functions)
If
holds true for every
Proof. Let
By Theorem 9.75,
The nonnegative homogeneity gives us
We are done.
9.8.14. Quasi-Convex Functions#
Definition 9.53 (Quasi convex function)
Let
If the sublevel sets