Compressive Sensing
Contents
18.7. Compressive Sensing#
In this section we formally define the problem of compressive sensing.
Compressive sensing refers to the idea that for sparse or compressible signals, a small number of nonadaptive measurements carry sufficient information to approximate the signal well. In the literature it is also known as compressed sensing and compressive sampling. Different authors seem to prefer different names.
In this section we will represent a signal dictionary
as well as its synthesis matrix as
A signal
and
The dictionary could be standard basis, Fourier basis, wavelet basis, a wavelet packet dictionary, a multi-ONB or even a randomly generated dictionary.
Real life signals are not sparse, yet they are compressible in the sense that
entries in the signal decay rapidly when sorted by magnitude.
As a result compressible signals are well
approximated by sparse signals.
Note that we are talking about the sparsity or compressibility
of the signal in a suitable dictionary.
Thus we mean that the signal
18.7.1. Definition#
Definition 18.24 (Compressive sensing)
In compressive sensing, a measurement is a linear functional applied to a signal
The compressive sensor makes multiple such linear measurements.
This can best be represented by the action of a sensing matrix
where
The vector
It is assumed that the signal
The objective is to recover
We do this by first recovering the sparse representation
If
The more interesting case is when
We note that given
We therefore can remove the dictionary from our consideration and look at
the simplified problem given as:
Recover
where

Fig. 18.13 A Gaussian sensing matrix of shape
18.7.2. The Sensing Matrix#
There are two ways to look at the sensing matrix. First view is in terms of its columns
where
i.e.,
This view looks very similar to a dictionary and its atoms but there is a difference.
In a dictionary, we require each atom to be unit norm.
We don’t require columns of the sensing matrix
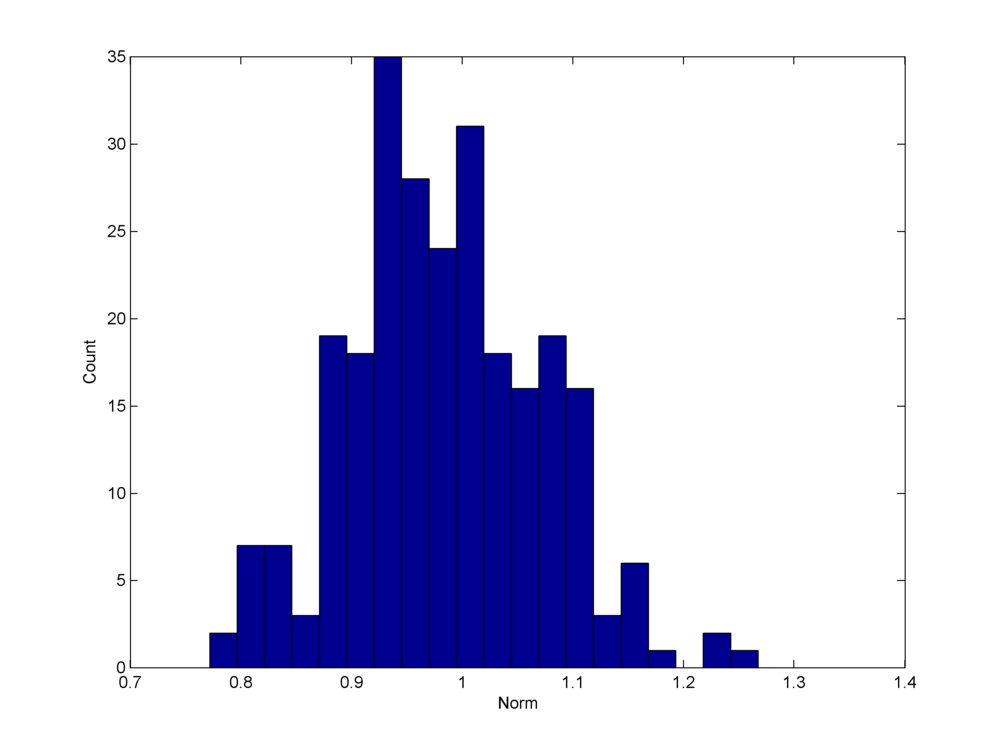
Fig. 18.14 A histogram of the norms of the columns of a Gaussian
sensing matrix. Although the histogram is strongly
concentrated around
The second view of sensing matrix
where
In this view
We will call
Definition 18.25 (Embedding of a signal)
Given a signal
Definition 18.26 (Explanation of a measurement)
A signal
Definition 18.27 (Measurement noise)
In real life, the measurement is not error free. It is affected by the presence of noise during measurement. This is modeled by the following equation:
where
Example 18.27 (Compressive measurements of a synthetic sparse signal )
In this example we show:
A synthetic sparse signal
Its measurements using a Gaussian sensing matrix
Addition of noise during the measurement process.
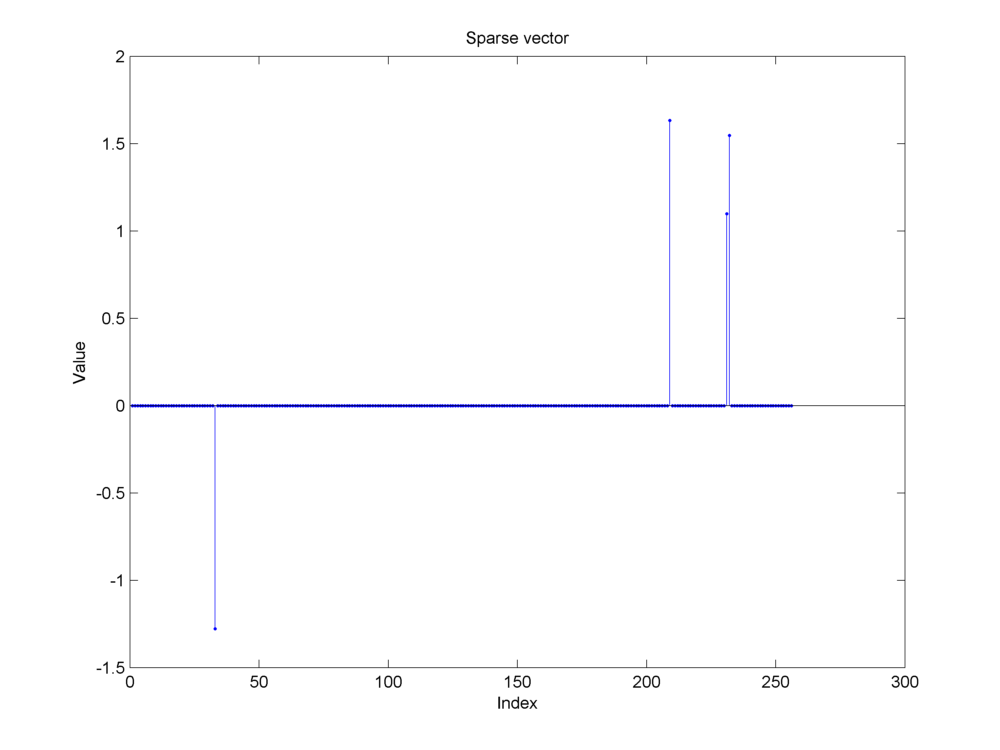
Fig. 18.15 A
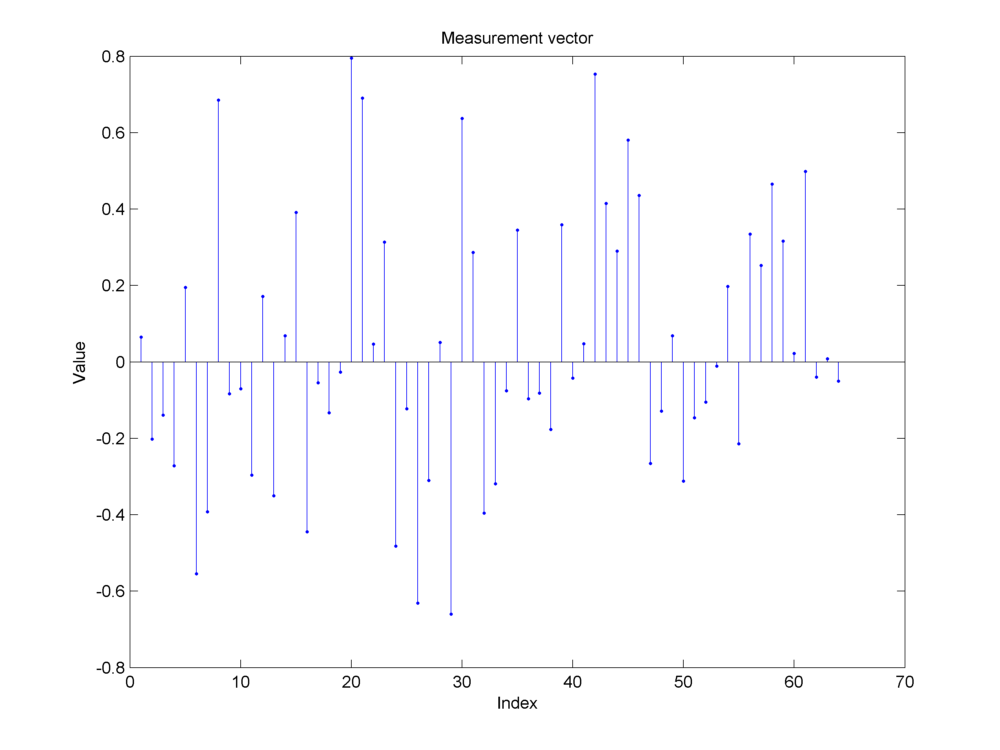
Fig. 18.16 Measurements made by a Gaussian sensing matrix
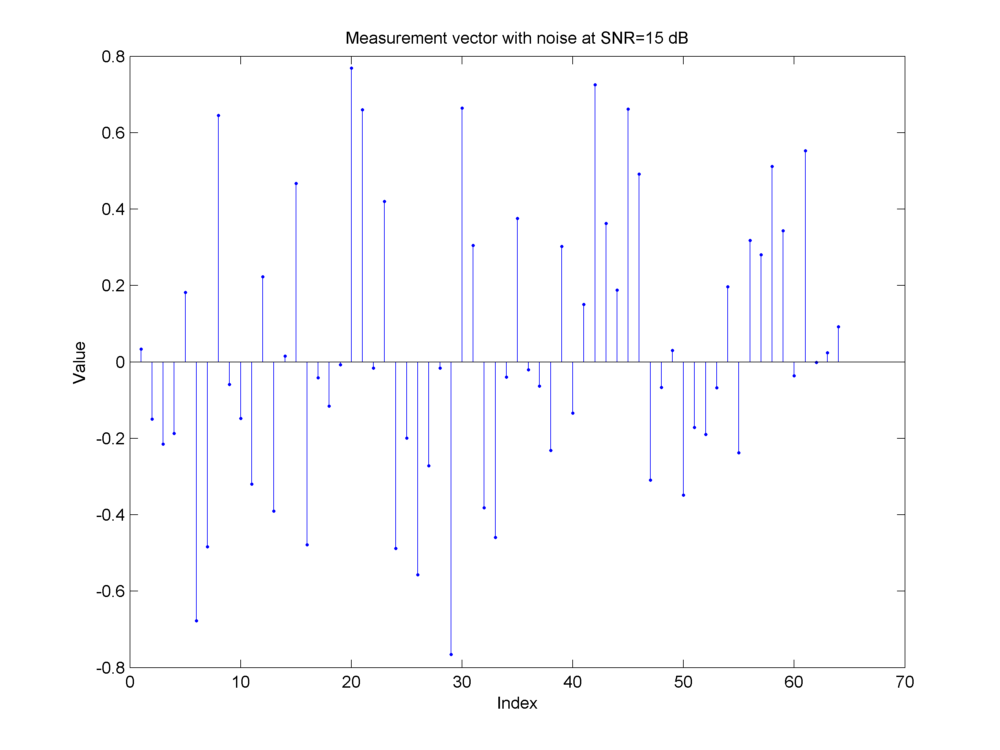
Fig. 18.17 Addition of measurement noise at an SNR of
In Example 18.30, we show the reconstruction of the sparse signal from its measurements.
In the following we present examples of real life problems which can be modeled as compressive sensing problems.
18.7.3. Error Correction in Linear Codes#
The classical error correction problem was discussed in one of the seminal founding papers on compressive sensing [19].
Example 18.28 (Error correction in linear codes as a compressive sensing problem)
Let
In order to make the message robust against errors in communication channel, we encode the error with an error correcting code.
We consider
where
We construct the “ciphertext”
where
where
is the left pseudo inverse of
The communication channel is going to add some error. What we actually receive is
where
The least squares solution by minimizing the error
Since
What is needed is an exact reconstruction of
To reconstruct
and from there
The question is: for a given sparsity level
The approach in [19] is as follows.
We construct a matrix
We then apply
Therefore the decoding problem is reduced to that of reconstructing
a sparse vector
With this the problem of finding
This now becomes the compressive sensing problem. The natural questions are
How many measurements
How should
How do we recover
These problems are addressed in following chapters as we discuss sensing matrices and signal recovery algorithms.
18.7.4. Piecewise Cubic Polynomial Signal#
Example 18.29 (Piecewise cubic polynomial signal)
This example was discussed in [18]. Our signal of interest is a piecewise cubic polynomial signal as shown below.

Fig. 18.18 A piecewise cubic polynomials signal#
It has a compressible representation in a wavelet basis.
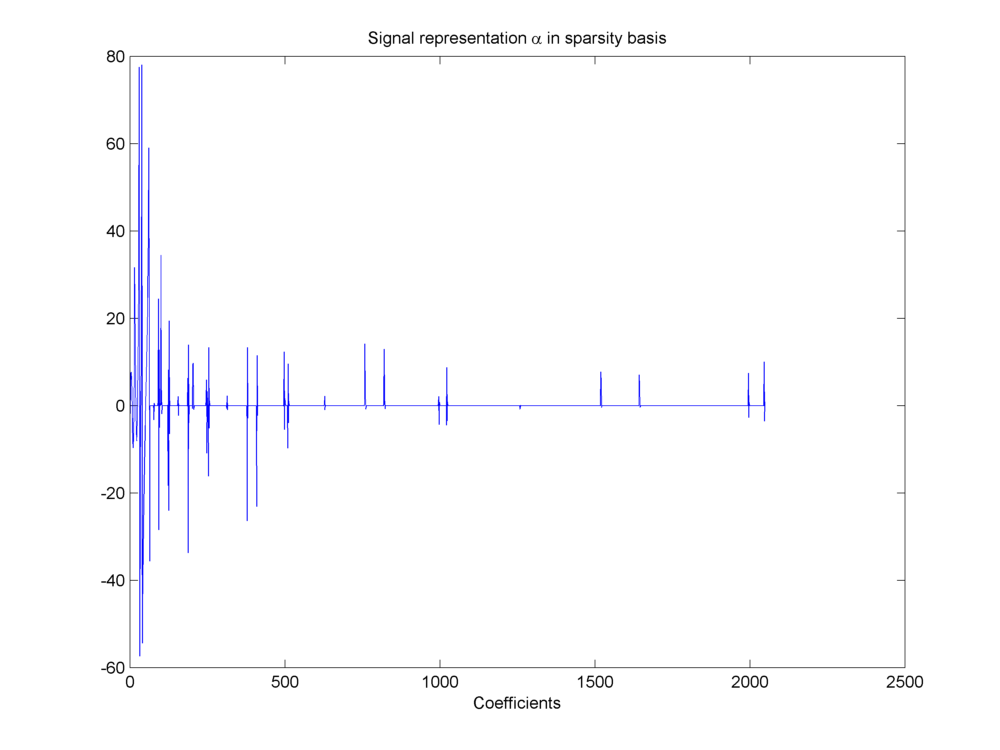
Fig. 18.19 Compressible representation of signal in wavelet basis#
The representation is described by the equation.
The chosen basis is a Daubechies wavelet basis
Fig. 18.20 Daubechies-8 wavelet basis#
In this example
We can sort the wavelet coefficients by magnitude and plot them in descending order to visualize how sparse the representation is.
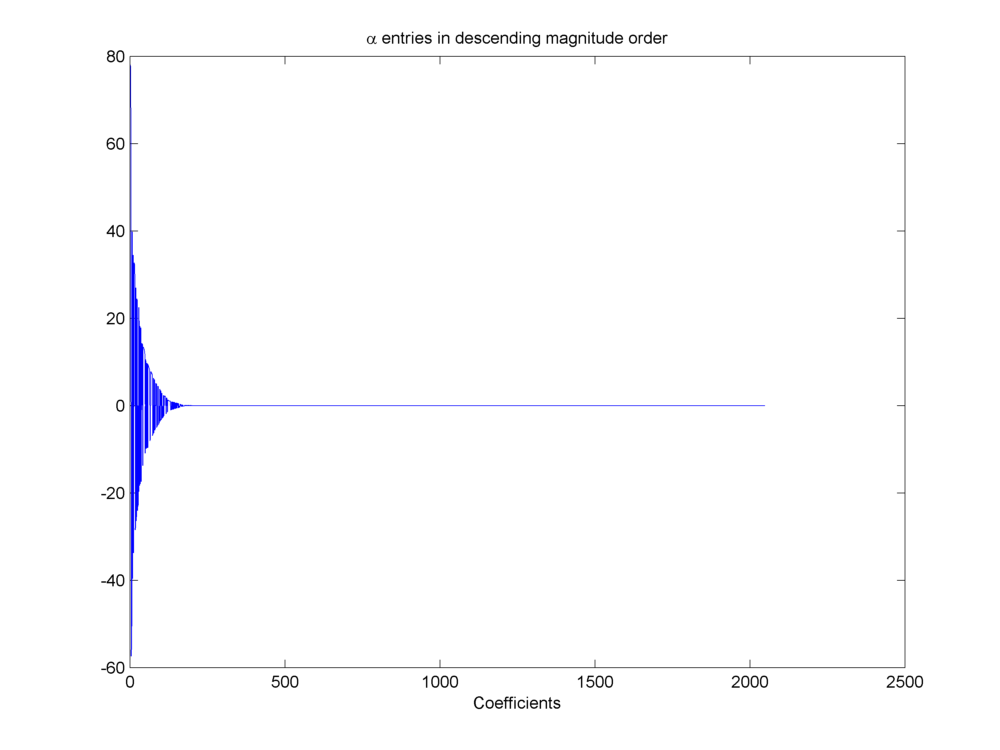
Fig. 18.21 Wavelet coefficients sorted by magnitude#
Before making compressive measurements, we need to decide how many compressive measurements will be sufficient?
Closely examining the coefficients in
Entries in wavelet representation of piecewise cubic polynomial signal higher than a threshold
Threshold |
Entries higher than threshold |
|---|---|
1 |
129 |
1E-1 |
173 |
1E-2 |
186 |
1E-4 |
197 |
1E-8 |
199 |
1E-12 |
200 |
A choice of
A Gaussian random sensing matrix
Fig. 18.22 Gaussian sensing matrix
The measurement process is described by the equation
with
The compressed measurements are shown below.

Fig. 18.23 Measurement vector
Finally the product of
Fig. 18.24 Recovery matrix
The sparse signal recovery problem is denoted as
where
18.7.5. Number of Measurements#
A fundamental question of compressive sensing framework is:
How many measurements are necessary to acquire
Clearly if
We further note that the sensing matrix
If the
In [20] Cand`es and Tao showed that the geometry of sparse signals should be preserved under the action of a sensing matrix. In particular the distance between two sparse signals shouldn’t change by much during sensing.
They quantified this idea in the form of a restricted isometric constant of a matrix
We will study more about this property known as restricted isometry property (RIP) in Restricted Isometry Property. Here we just sketch the implications of RIP for compressive sensing.
When
Further if
It is now known that many randomly generated matrices have excellent RIP behavior.
One can show that if
measurements, one can recover
Some of the typical random matrices which have suitable RIP properties are
Gaussian sensing matrices
Partial Fourier matrices
Rademacher sensing matrices
18.7.6. Signal Recovery#
The second fundamental problem in compressive sensing is:
Given the compressive measurements
A simple formulation of the problem as:
minimize
Over the years, people have developed a number of algorithms to tackle the sparse recovery problem.
The algorithms can be broadly classified into following categories
[Greedy pursuits] These algorithms attempt to build the approximation of the signal iteratively by making locally optimal choices at each step. Examples of such algorithms include OMP (orthogonal matching pursuit), stage-wise OMP, regularized OMP, CoSaMP (compressive sampling pursuit) and IHT (iterative hard thresholding).
[Convex relaxation] These techniques relax the
[Combinatorial algorithms] These methods are based on research in group testing and are specifically suited for situations where highly structured measurements of the signal are taken. This class includes algorithms like Fourier sampling, chaining pursuit, and HHS pursuit.
A major emphasis of these notes will be the study of these sparse recovery algorithms. We shall provide some basic results in this section. We shall work under the following framework in the remainder of this section.
Let
Let us make
The measurements are given by
We assume that measurements are non-adaptive; i.e., the matrix
The recovery process is denoted by
where
We will look at three kinds of situations:
Signals are truly sparse. A signal has up to
Signals are not truly sparse but they have few
Signals are not sparse. Also there is measurement noise being introduced. We expect recovery algorithm to minimize error and thus perform stable recovery in the presence of measurement noise.
Example 18.30 (Reconstruction of the synthetic sparse signal from its noisy measurements)
Continuing from Example 18.27, we show the approximation reconstruction of the synthetic sparse signal using 3 different algorithms.
Basis pursuit (
Matching pursuit algorithm
Orthogonal matching pursuit algorithm
The reconstructions are not exact due to the presence of measurement noise.
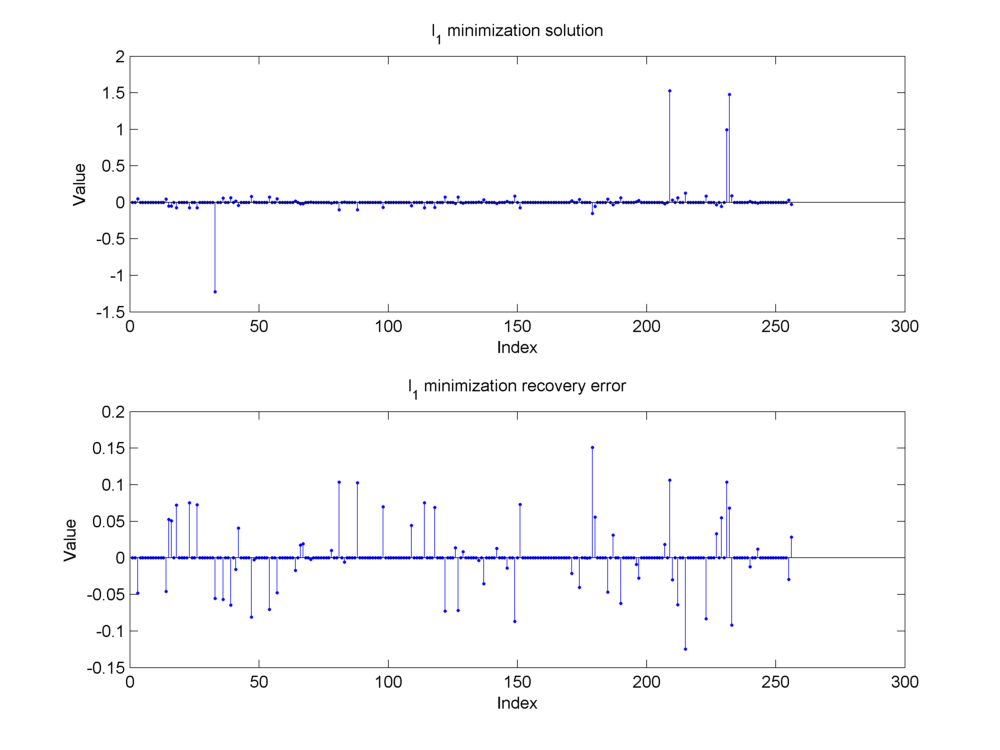
Fig. 18.25 Reconstruction of the sparse signal using
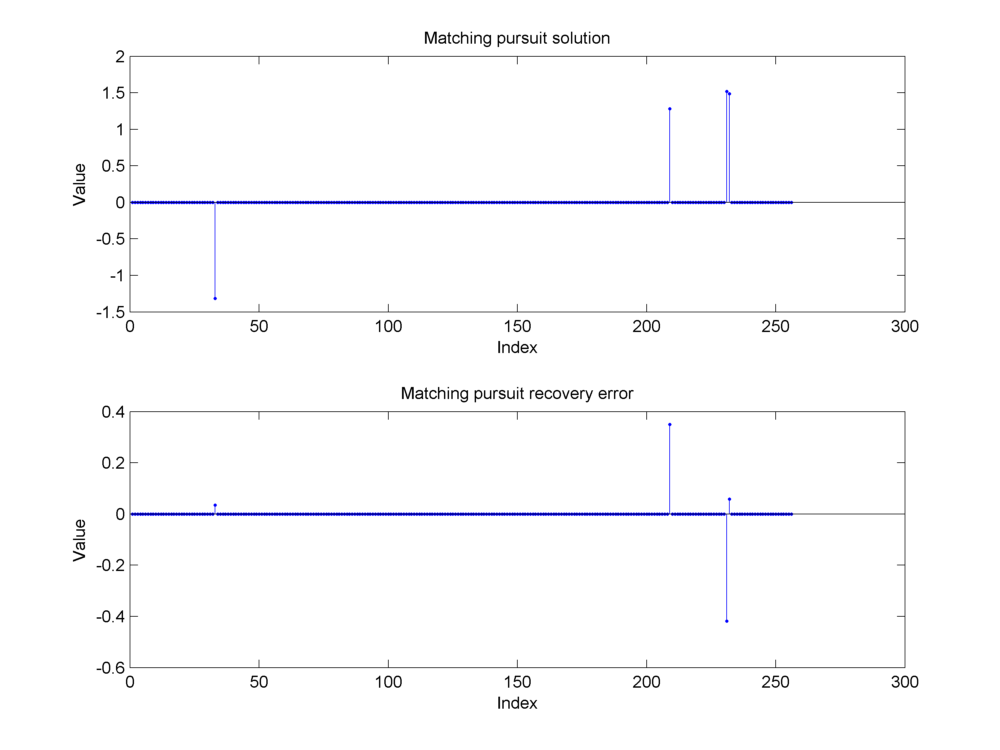
Fig. 18.26 Reconstruction of the sparse signal using matching pursuit. The support of the original signal has been identified correctly but matching pursuit hasn’t been able to get the magnitude of these components correctly. Some energy seems to have been transferred between the nearby second and third nonzero components. This is clear from the large magnitude in the recovery error at the second and third components. The presence of measurement noise affects simple algorithms like matching pursuit severely.#
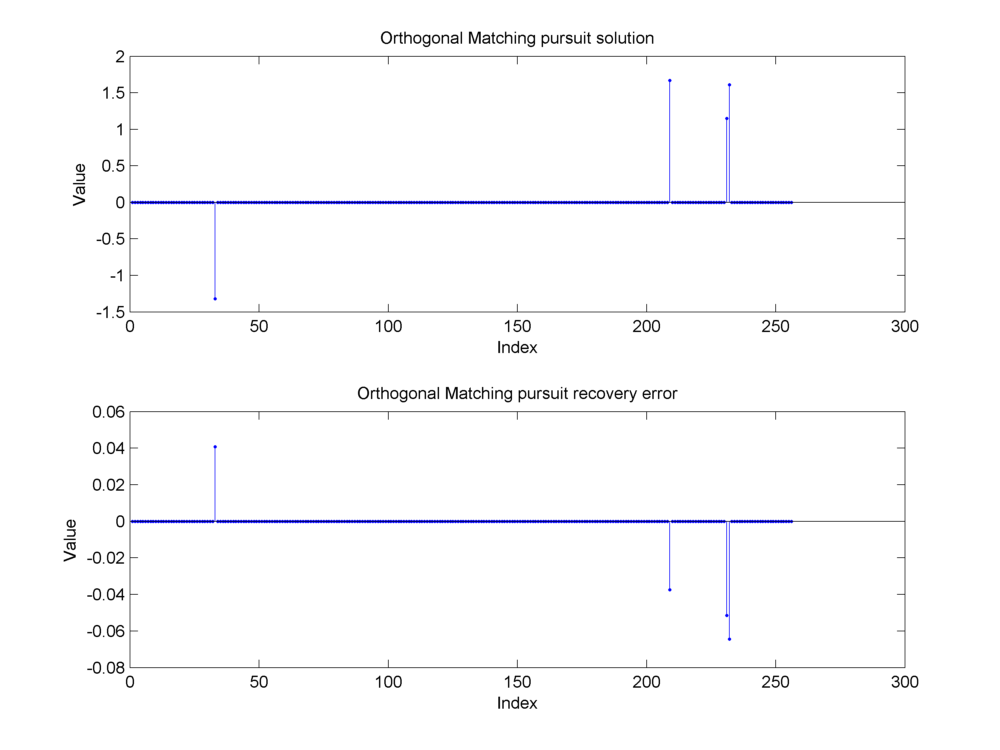
Fig. 18.27 Reconstruction of the sparse signal using orthogonal matching pursuit. The support has been identified correctly and the magnitude of the nonzero components in the reconstructed signal is close to the original signal. The reconstruction error is primarily due to the presence of measurement noise. It is roughly evenly distributed between all the nonzero entries since orthogonal matching pursuit computes a least squares solution over the selected indices in the support.#
18.7.7. Exact Recovery of Sparse Signals#
The null space of a matrix
The set of
Example 18.31 (K sparse signals)
Let
Lemma 18.2
If
Proof.
Example 18.32 (Difference of K sparse signals)
Let N = 5.
Let
Let
Let
Definition 18.28 (Unique embedding of a set)
We say that a sensing matrix
Theorem 18.38 (Unique embeddings of
A sensing matrix
Proof. We first show that the difference of sparse signals is not in the nullspace.
Let
Then
Now if
Thus
Thus
We show the converse by contradiction.
Let
Thus
Then we can find
Thus there exists
But then,
There are equivalent ways of characterizing this condition. In the following, we present a condition based on spark.
18.7.7.1. Spark#
We recall from Definition 18.17, that spark of a matrix
Theorem 18.39 (Unique explanations and spark)
For any measurement
Proof. We need to show
If for every measurement, there is only one
If
Assume that for every
Now assume that
Thus there exists a set of at most
Thus there exists
Thus
Thus
Hence
Hence
Now suppose that
Assume that for some
Then
Thus
Hence, there exists a set of at most
Thus
Hence, for every
Since
18.7.8. Recovery of Approximately Sparse Signals#
Spark is a useful criteria for characterization of sensing matrices for truly sparse signals.
But this doesn’t work well for approximately sparse signals.
We need to have more restrictive criteria on
In this context we will deal with two types of errors:
Approximation error
Let us approximate a signal
Let us call the approximation as
Thus
Recovery error
Let
Let
Then
The error
Ideally, the recovery error should not be too large compared to the approximation error.
In this following we will
Formalize the notion of null space property (NSP) of a matrix
Describe a measure for performance of an arbitrary recovery algorithm
Establish the connection between NSP and performance guarantee for recovery algorithms.
Suppose we approximate
One specific
In the following, we will need some additional notation.
Let
Let
Let
Example 18.33
Let N = 4.
Then
Let
Then
Now let
Then
Example 18.34
Let N = 4.
Then
Let
Then
Now let
Then
Now let
Then
18.7.8.1. Null Space Property#
Definition 18.29 (Null space property)
A matrix
holds for every
Let
Essentially vectors in
If
18.7.8.2. Measuring the Performance of a Recovery Algorithm#
Let
The
We will be interested in guarantees of the form
Why, this recovery guarantee formulation?
Exact recovery of K-sparse signals.
Robust recovery of non-sparse signals
Recovery dependent on how well the signals are approximated by
Such guarantees are known as instance optimal guarantees.
Also known as uniform guarantees.
Why the specific choice of norms?
Different choices of
If an algorithm
We show that NSP of order
18.7.8.3. NSP and Instance Optimal Guarantees#
Theorem 18.40 (NSP and instance optimal guarantees)
Let
Proof. We are given that
Together, they satisfy instance optimal guarantee (18.39).
Thus they are able to recover all sparse signals exactly.
For non-sparse signals, they are able to recover their
We need to show that if
where
Let
Let
Then
Split
We have
Let
Let
Then
By assumption
Thus
But since
Thus
i.e., the recovery algorithm
Certainly
Hence
Finally we also have
since
But as per instance optimal recovery guarantee (18.39) for
Thus
But
Recall that
Hence the best
Hence
Thus we finally have
Thus
It turns out that NSP of order
18.7.9. Recovery in Presence of Measurement Noise#
Measurement vector in the presence of noise is given by
where
Recovery error as usual is given by
Stability of a recovery algorithm is characterized by comparing variation of recovery error w.r.t. measurement error.
NSP is both necessary and sufficient for establishing guarantees of the form:
These guarantees do not account for presence of noise during measurement.
We need stronger conditions for handling noise. The restricted isometry property for sensing matrices comes to our rescue.
18.7.9.1. Restricted Isometry Property#
We recall that a matrix
holds for every
If a matrix satisfies RIP of order
If a matrix satisfies RIP of order
We say that the matrix is nearly orthonormal for sparse vectors.
If a matrix satisfies RIP of order
18.7.9.2. Stability#
Informally a recovery algorithm is stable if recovery error is small in the presence of small measurement noise.
Is RIP necessary and sufficient for sparse signal recovery from noisy measurements? Let us look at the necessary part.
We will define a notion of stability of the recovery algorithm.
Definition 18.30 (
Let
Error is added to the measurements.
LHS is
RHS consists of scaling of the
The definition says that recovery error is bounded by a multiple of the measurement error.
Thus adding a small amount of measurement noise shouldn’t be causing arbitrarily large recovery error.
It turns out that
Theorem 18.41 (Necessity of RIP for
If a pair
for all
Proof. Remember that any
Let
Split it in the form of
Define
Thus
We have
Also we have
Let
Since
Also
Using the triangle inequality
Thus we have for every
This theorem gives us the lower bound for RIP property of
order
Note that smaller the constant
This result doesn’t require an upper bound on the RIP property in (18.38).
It turns out that If
18.7.9.3. Measurement Bounds#
As stated in previous section, for a
Before we start figuring out the bounds, let us develop a special subset of
When we say
Hence
Example 18.35 (
Each vector in
Revisiting
It is now obvious that
Since there are
By definition
Further Let
Then
We now state a result which will help us in getting to the bounds.
Lemma 18.3
Let
and
Proof. We just need to find one set
First condition states that the set
We will construct
Since
Consider any fixed
How many elements
Define
Clearly by requirements in the lemma, if
How many elements are there in
If
Hence if
So define
We have
Thus we have an upper bound given by
Let us look at
We can choose
At each of these
Thus we have an upper bound
We now describe an iterative process for building
Say we have added
Then
Number of vectors in
Thus we have at least
vectors left in
We can keep adding vectors to
We can construct a set of size
Now
Note that
Its minimum value is achieved for
So we have
Rephrasing the bound on
Hence we can definitely construct a set
Now it is given that
Thus we have
Choose
Clearly this value of
Hence
Thus
which completes the proof.
We can now establish following bound on the required number of measurements to satisfy RIP.
At this moment, we won’t worry about exact value of
Theorem 18.42 (Minimum number of required measurements for RIP of order
Let
where
Proof. Since
Also
Consider the set
Also
since
and an upper bound:
What do these bounds mean? Let us start with the lower bound.
Construct
Lower bound says that these balls are disjoint.
Since
Upper bound tells us that all vectors
Thus the set of all balls lies within a larger ball of radius
So we require that the volume of the larger ball MUST be greater than the sum of volumes of
Since volume of an
Again from Lemma 18.3 we have
Putting back we get
which establishes a lower bound on the number of measurements
Example 18.36 (Lower bounds on
Some remarks are in order:
The theorem only establishes a necessary lower bound on
The restriction
This result fails to capture dependence of
We haven’t made significant efforts to optimize the constants. Still they are quite reasonable.
18.7.10. RIP and NSP#
RIP and NSP are connected.
If a matrix
Thus RIP is strictly stronger than NSP (under certain conditions).
We will need following lemma which applies to any arbitrary
Lemma 18.4
Suppose that
Define
where
Let us understand this lemma a bit.
If
Thus
We now state the connection between RIP and NSP.
Theorem 18.43
Suppose that
Proof. We are given that
holds for all
holds
Let
Then
Let
Then
Similarly
Thus if we show that
then we would have shown it for all
Hence let
We can divide
Since
Hence as per Lemma 18.4 above, we have
Also
Thus we have
We have to get rid of
Since
Hence
But since
Hence
Note that the inequality is also satisfied for
Now
Putting
we see that
Note that for