Sparsity in Orthonormal Bases
Contents
18.4. Sparsity in Orthonormal Bases#
We start this section with a quick review of orthonormal bases and
orthogonal transforms for finite dimensional
signals
We present an uncertainty principle which explains why a pair of orthonormal bases (like Dirac and Fourier basis) cannot have sparse representation of the same signal simultaneously.
We then demonstrate that a combination of two orthonormal bases can be quite useful in creating a redundant yet sparse representation of a larger class of signals which could not be sparsely represented in either of the two bases individually.
This motivates us to discuss more general over-complete signal dictionaries in the next section.
18.4.1. Orthonormal Bases and Orthogonal Transforms#
In signal processing, we often convert a finite length time domain signal into a different domain using finite length transforms. Some of the most common transforms are discrete Fourier transform, the discrete cosine transform, and the Haar transform. They all belong to the class of transforms called orthogonal transforms.
Orthogonal transforms are characterized by a pair of equations
and
where
then
In other words:
Eq. (18.5) is known as
the synthesis equation (
This result is commonly known as Parseval’s identity in signal processing community.
More generally, orthogonal transforms preserve inner products:
Example 18.7 (Dirac basis and sparse signals)
The simplest orthogonal transform is the identity basis or the standard ordered
basis for
We have
In this basis
We will drop
This basis is also known as Dirac basis. The name Dirac comes from the Dirac delta functions used in signal analysis in continuous time domain.
The basis consists of finite length impulses denoted by
If a signal
is
can be expressed as a linear combination of just 3 impulses.
In contrast if we consider a complex sinusoid in
18.4.2. Fourier Basis and Sparse Signals#
The most popular finite length orthogonal transform is DFT (Discrete Fourier Transform).
We define the
Clearly
We define the synthesis matrix of DFT as
where
The definition is symmetric. Hence
Note that we have multiplied with
The columns of
Example 18.8 (Fourier basis for
2nd root of unity is given by
Hence
In this case
Example 18.9 (Fourier basis for
3rd root of unity is given by
Hence
In this case
Example 18.10 (Fourier basis for
4th root of unity is given by
Hence
In this case
We drop the suffix
If a signal
Example 18.11 (Sparse signals in
Consider the following signal
Its representation in
Clearly the signal is
Now consider a signal
Its representation in
Thus we see that while
18.4.3. An Uncertainty Principle#
As we noted, Dirac basis can give sparse representations for impulses but not for complex sinusoids. Vice versa Fourier basis can give sparse representations for complex sinusoids but not impulses.
Can we claim that a signal cannot be simultaneously represented both in time (Dirac basis) and in frequency domain (Fourier basis)?
More generally, let
where
The answer turns out to be yes, but it depends on how much the two bases are similar or close to each other. The results in this section were originally developed in [31].
Definition 18.1 (Proximity/Mutual coherence)
The proximity between two orthonormal bases
and
is defined as the maximum absolute value of inner products between the columns of these two bases:
This is also known as mutual coherence of the two orthonormal bases.
If the two bases are identical, then clearly
If the vectors in
Example 18.12 (Proximity or mutual coherence of Dirac and Fourier bases)
Consider the mutual coherence between Dirac and Fourier bases.
For some small values of
N |
|
|---|---|
2 |
0.7071 |
4 |
0.5000 |
6 |
0.4082 |
8 |
0.3536 |
For larger values of
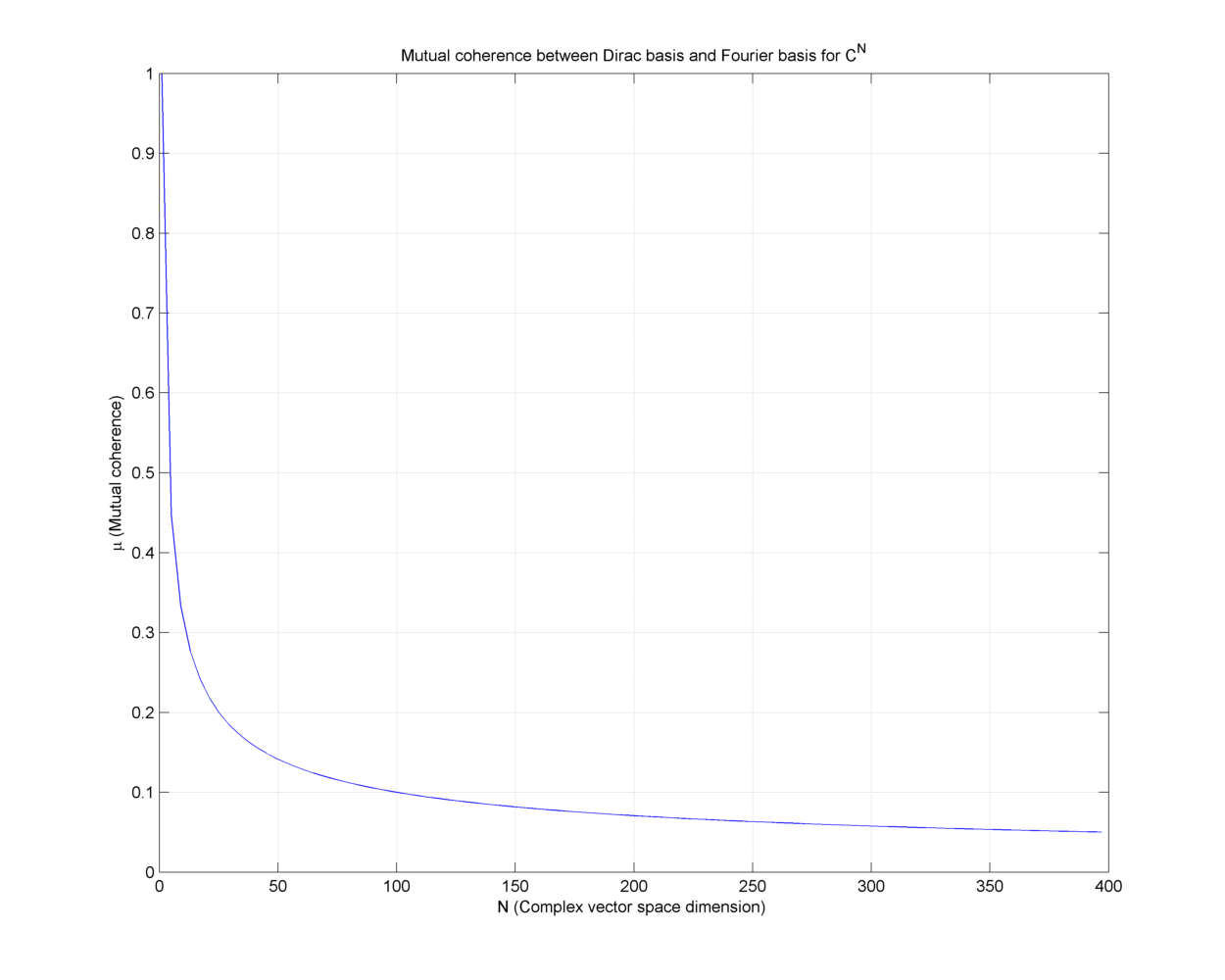
Fig. 18.4 Mutual coherence for Dirac and Fourier bases#
We present some results related to mutual coherence of two orthonormal bases.
Theorem 18.2 (Product of orthonormal bases)
The product of two orthonormal bases
Proof. Consider the matrix
Any column of the product matrix is
But then
Thus each column of the product
Consider the inner product of two columns of
Thus, the columns of
Hence
Remark 18.3 (The group of orthonormal bases)
A more general result would be to show that the set of orthonormal bases forms a group under the matrix multiplication operation. The identity element is the Dirac basis. The inverse of an orthonormal basis is also an orthonormal basis. The product of two orthonormal bases is also an orthonormal basis. The matrix multiplication satisfies associative law.
Theorem 18.3 (Mutual coherence bounds)
Mutual coherence of two orthonormal bases
Proof. Since columns of both
Now if
Now consider the matrix
Since the column is unit norm, hence some of squares of the absolute values of entries of the column is 1.
Thus the absolute value of each of the entries cannot be simultaneously less than
Hence there exists an entry (in each column) such that
Hence we get the lower bound on mutual coherence of
Theorem 18.4 (Mutual coherence of Dirac and Fourier bases)
Mutual coherence of Dirac and Fourier bases is
Proof. Theorem 18.3 shows that
We just need to show that its in fact an equality.
Consider
Consider
where
This doesn’t depend on the choice of
With basic properties of mutual coherence in place, we are now ready to state
an uncertainty principle on the sparsity levels of representations of same signal
Theorem 18.5 (Uncertainty principle)
For any arbitrary pair of orthonormal bases
Moreover for unit-length
Proof. Dividing
Hence without loss of
generality, we will assume that
We are given that
We can write
where we note that
and
Hence we get the inequality
Using the inequality between algebraic mean and geometric mean
we get
This is an uncertainty principle for the
Consider the sets
and
Clearly
The representations
This can be written as an optimization problem of the form
Let the optimal solution for this problem be
Similarly from the set
Let the optimal solution for this problem be
Returning back to the inequality
we can write
An equivalent formulation of the optimization problem (18.10)is
This formulation doesn’t require any specific mention of the basis
Here we consider the optimization problem to be parameterized by the
Then by symmetry, optimal value for the problem (18.11) is
Thus we can write
This is our intended result since we have been able to write the inequality as
a function of
In order to complete the result, we need to find the solution of the
optimization problem (18.12) given
by the function
Without loss of generality, let us assume that the
Let us further assume that all non-zero entries of
Using Lagrange multipliers, the
Differentiating w.r.t.
The
Thus
and
Thus the optimal value of the optimization problem (18.12) is
Similarly
Putting back in (18.13) we get
Applying the algebraic mean-geometric mean inequality we get the desired result
This theorem suggests that if two orthonormal bases have low mutual coherence then
the two representations for
the two representations for
Challenge
Can we show that the above result is sharp? i.e. For a pair of orthonormal bases
Example 18.13 (Sparse representations with Dirac and Fourier bases)
We showed in Theorem 18.4 that
Let
Applying Theorem 18.5 we have
This tells us that a signal cannot have fewer than
18.4.4. Linear Combinations of Impulses and Sinusoids#
What happens if a signal
The set of sinusoids and impulses involved in the construction of
In absence of prior knowledge of component signals of
While the Dirac basis can provide sparse representation for impulses, sinusoids have dense representation in Dirac basis. Vice versa, in Fourier basis, complex sinusoids have sparse representation, yet impulses have dense representations. Thus neither of the two bases is capable of providing a sparse representation for a combination of impulses and sinusoids.
The natural question arises if there is a way to come up with a sparse representation for such signals by combining the Dirac and Fourier basis?
18.4.5. Dirac Fourier Basis#
Now we develop a representation of signals
We define a new synthesis matrix
We can write
and
This enables us to write
We will look for a representation of
where
Since this representation is under-determined and
We would prefer to choose the sparsest representation which can be stated as an optimization problem
Example 18.14 (Sparse representation using Dirac Fourier Basis)
Let
Let
A sparse representation of
This representation is
Thus we see that Dirac Fourier basis is able to provide a sparser representation of a linear combination of impulses and sinusoids compared to individual orthonormal bases (the Dirac basis and the Fourier basis).
This gives us motivation to consider such combination of bases which help us provide a sparse representation to a larger class of signals. This is the objective of the next section.
In due course we will revisit the Dirac Fourier basis further in several examples.
18.4.6. Two-Ortho Basis#
Before we leave this section, let us define general two-ortho bases.
Definition 18.2 (Two ortho basis)
Let
We define
The columns of
Clearly columns of
Remark 18.4 (Coherence of a two ortho basis)
The coherence of a two ortho basis is defined as
It is the magnitude of the largest inner product between
columns of
We present a very interesting result about the null space of
Theorem 18.6 (Denseness of vectors in null space of two ortho bases)
For a two ortho basis
Concretely
Proof. Let
Now let
If
We note that
Applying Theorem 18.5 we have
We also note that since the orthonormal bases preserve norm, hence
This shows us that the energy of a null space vector is evenly distributed in the two components corresponding to each orthonormal basis.
Challenge
For a two-ortho basis
Let
Obviously for every
What we are particularly interested in are sparse representations of
Formally, let
This is established in the next uncertainty principle.
Theorem 18.7 (Uncertainty principle for representations in two ortho basis)
Let
Then the following holds
This is an uncertainty principle for the sparsity of distinct representations in two ortho basis.
Proof. Let
be the difference vector of representations of
Thus
But since
Challenge
For a two-ortho basis
This theorem suggests as that if
Rather if a representation is sufficiently sparse, then all other representations
of
This is stated formally in the following uniqueness theorem.
Theorem 18.8 (Uniqueness of sparse representation in two ortho basis)
If a representation of
Proof. Let
Let
This gives us
Thus we find that
which is true for every representation
Hence
We note here that any arbitrary choice of two bases may not be helpful in coming up with a two ortho basis which can provide us sparse representations for our signals of interest. In next few sections, we will explore this issue further in the more general context of signal dictionaries.
Challenge
Clearly, are signals for which a sufficiently sparse (and unique) representation doesn’t exist in a given two-ortho basis. What kind of relationships may exist between different (insufficiently) sparse representations of such signals?
18.4.7. Dirac-DCT Basis#
Dirac Fourier 2-ortho-basis is optimal in the sense that it has the smallest mutual coherence between the two bases. However, one problem with the Dirac Fourier basis is that it requires us to work with complex numbers. A close second is the Dirac DCT basis which consists of the Dirac basis and the DCT basis both of which are real.
Definition 18.3 (Dirac DCT basis)
The Dirac-DCT basis is a two-ortho basis consisting of the union of the Dirac and the DCT bases.
This two ortho basis is suitable for real signals since both
Dirac and DCT are totally real bases
The two ortho basis is obtained by combining the
Let
Let
The
with
Note that for
Thus, the
18.4.7.1. Example#
We show how a mixture signal consisting of impulses and sinusoids has a sparse representation in a Dirac DCT basis.
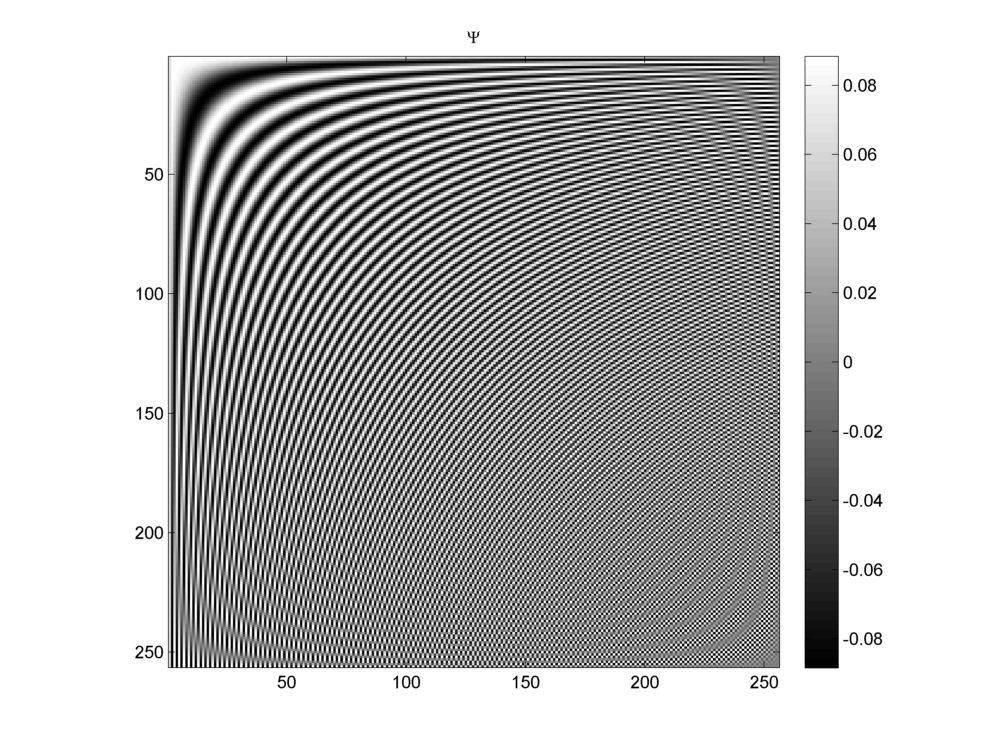
Fig. 18.5 A DCT basis for
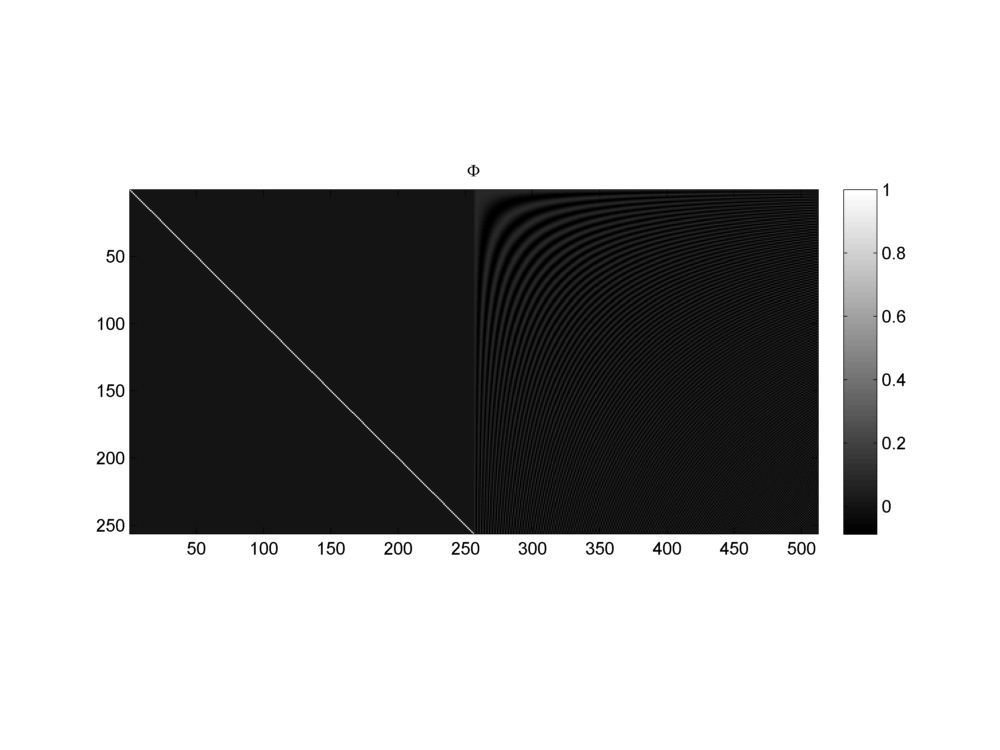
Fig. 18.6 A Dirac DCT basis for
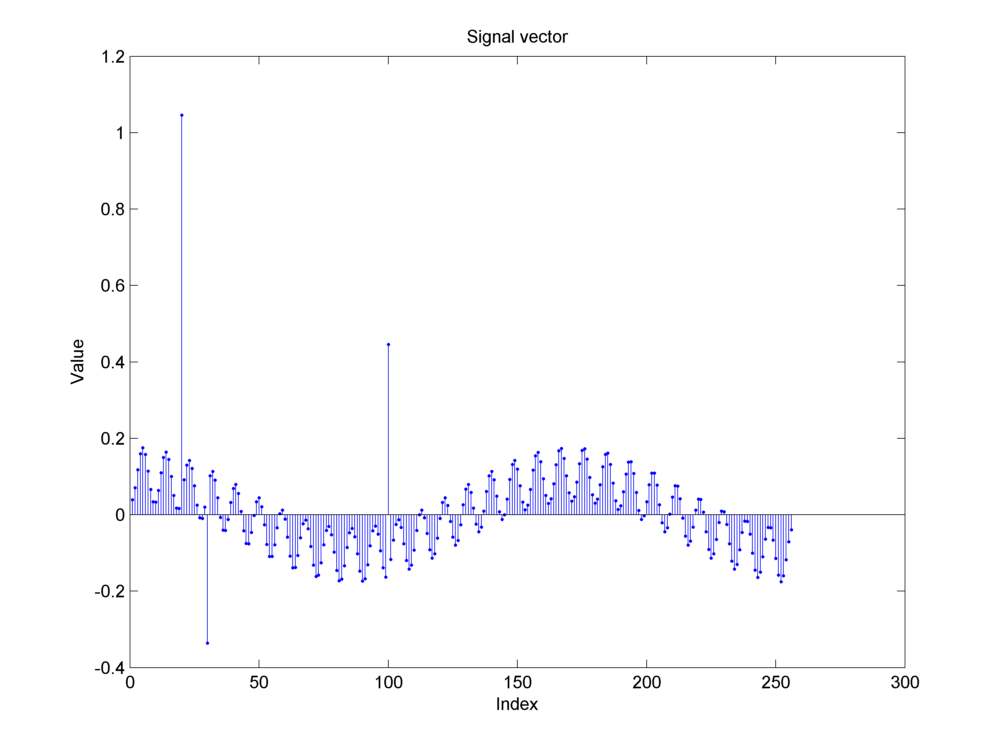
Fig. 18.7 An
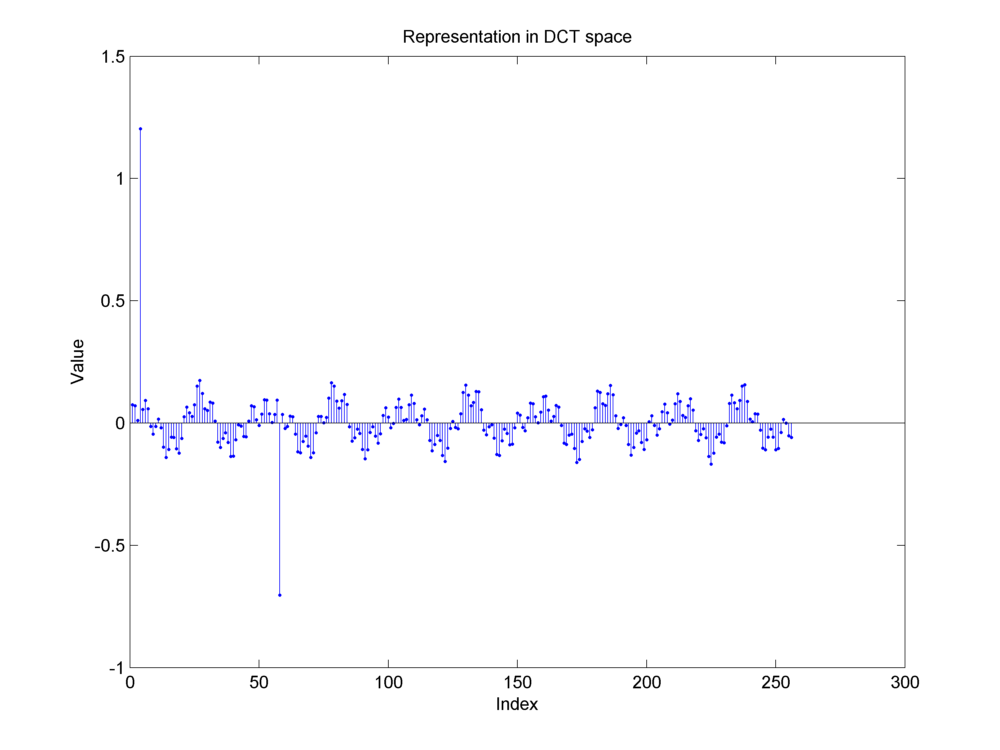
Fig. 18.8 Representation of the same mixture signal in DCT basis. Notice the two large magnitude components. They correspond to the two sinusoidal components in the original time domain signal. The three impulses in the time domain signal have been distributed among all the frequencies.#

Fig. 18.9 A sparse representation of the same mixture signal in the two ortho Dirac-DCT basis. The three impulses from the original signal appear on the left half (corresponding to the Dirac basis part). The two cosine sinusoids appear on the right half (corresponding to the DCT basis part). Indeed the representation is not unique. But it is the unique sparsest possible representation. All other representations have far more nonzero components.#
18.4.7.2. Coherence#
Theorem 18.9
The Dirac-DCT basis has the mutual coherence of
Proof. The mutual coherence of a two ortho basis where one basis is Dirac basis is given by the magnitude of the largest entry in the other basis.
For
Clearly,
18.4.7.3. Construction of Sparse Representation#
We use sparse recovery/reconstruction algorithms to construct a sparse representation of a given signal in a two ortho basis. The algorithms will be discussed in later chapters. We give the time domain signal (e.g. the mixture signal above) and the two ortho basis to a sparse reconstruction algorithm. The algorithm attempts to construct a sparsest possible representation of the signal in the given two ortho basis. We reconstructed this mixture signal in Dirac DCT basis using three different algorithms:
Basis Pursuit
Matching Pursuit
Orthogonal Matching Pursuit
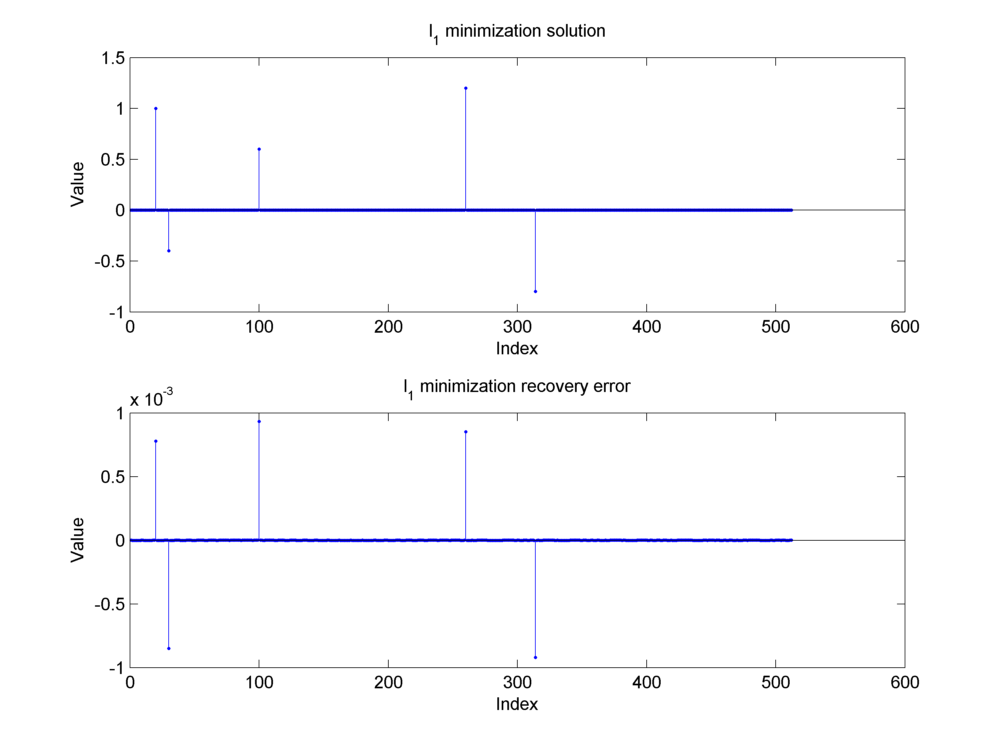
Fig. 18.10 Construction of the sparse representation of the mixture signal using the basis pursuit algorithm.#
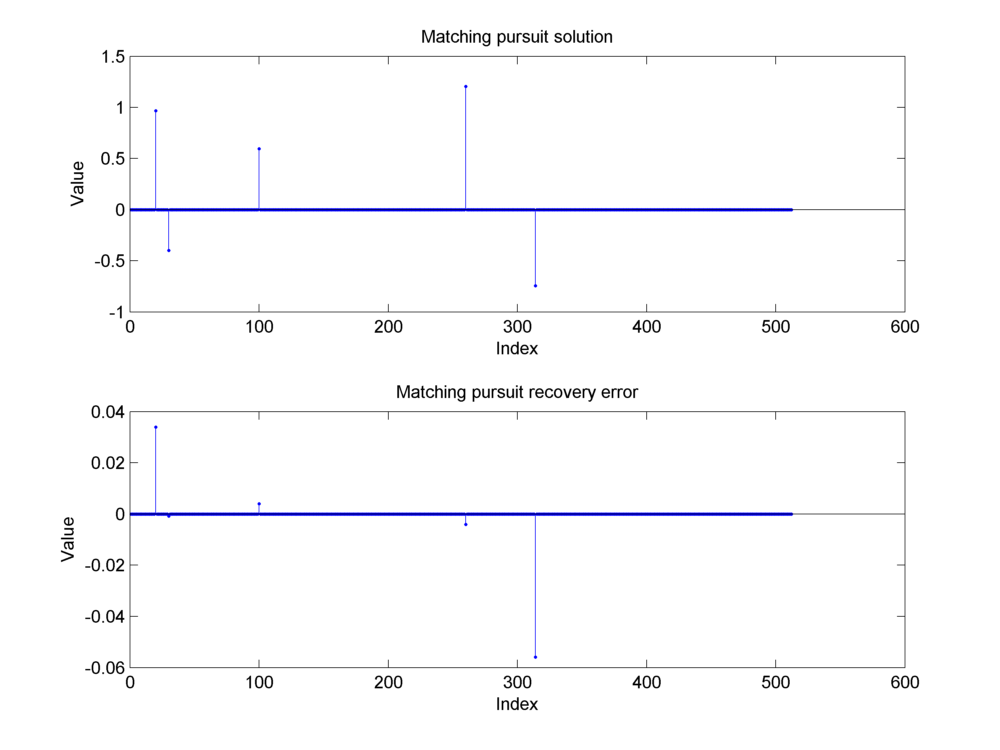
Fig. 18.11 Construction of the sparse representation of the mixture signal using the matching pursuit algorithm.#
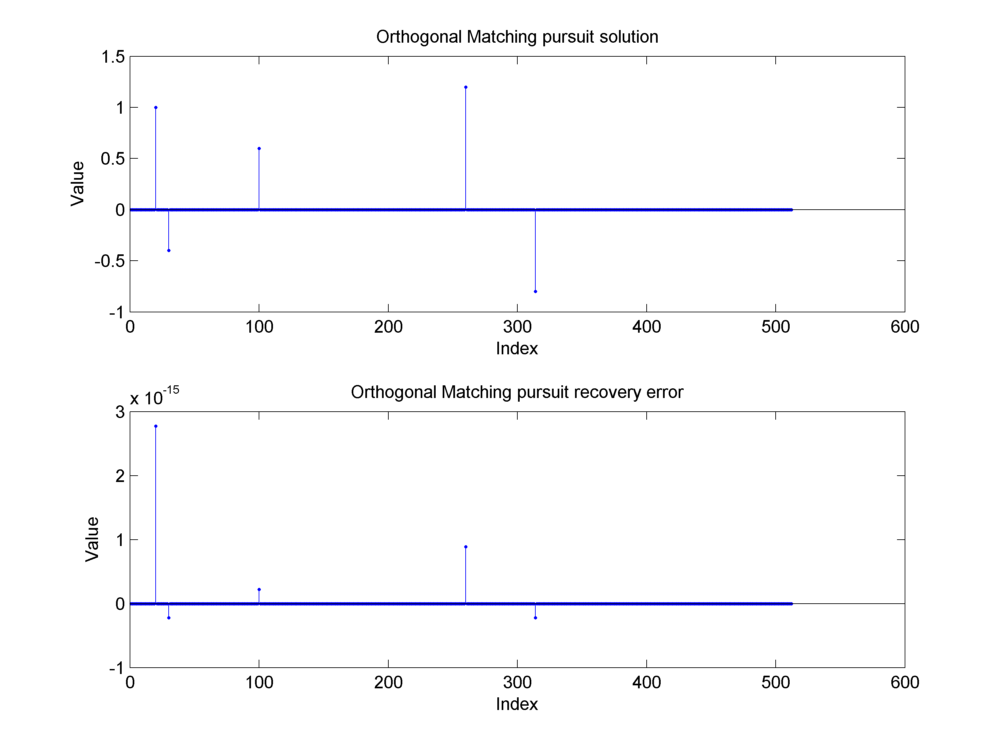
Fig. 18.12 Construction of the sparse representation of the mixture signal using the orthogonal matching pursuit algorithm.#